|
Aristide Cavaillé-Coll
ne nous a pas laissé un "traité" au sens propre
du terme, mais des études dont une, sur les tuyaux d'orgues, vient
préciser les trouvailles de ses prédécesseurs, notamment
le Physicien Bernoulli (qu'il orthographie "Bernouilli"). En
1840.
L'étude sur les tuyaux d'orgues est publiée sur le site :
http://perso.club-internet.fr/smcj/bureau/biblio/cavaille/etd_tuy/tit_txt.htm
il est donc inutile d'y revenir ici.
Vingt ans plus tard,
en 1860, Aristide Cavaillé-Coll fit une communication à
l'Académie des Sciences de Paris pour faire part de ses observations
concernant la correspondance entre la longueur physique du résonateur
des tuyaux d'orgues, et la longueur d'onde émise, en fonction de
la section de ces tuyaux.
Il énonce une formule de correction de la longueur du tuyau en
fonction de sa profondeur, pour les tuyaux carrés, et du diamètre
pour les tuyaux ronds.
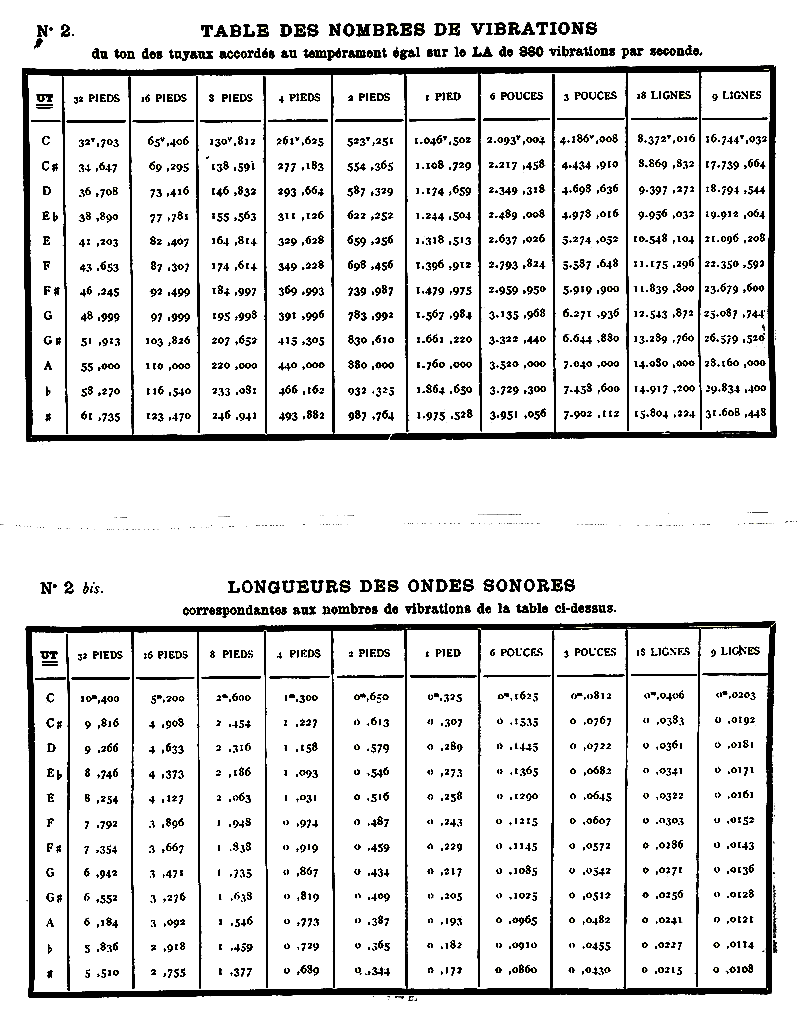
Il complète
cette communication par un tableau de la longueur de l'onde sonore de
tous les tuyaux pour différentes tonalités de diapason.
Longueur qu'il y aura lieu de corriger par la formule de correction pour
obtenir la longueur réelle du résonateur.
Je publie ici le tableau correspondant à un La 440 Hz, qu'il
dénomme "880 vibrations par secondes".
DE LA DÉTERMINATION
DES DIMENSIONS DES TUYAUX
PAR RAPPORT A LEUR INTONATION (1)
« Dans une série d'expériences
faites en vue de déter-
miner exactement les sons harmoniques des tuyaux
d'orgues, dans le but de créer des nouveaux jeux avec
des séries de tuyaux donnant leurs harmoniques au lieu
du son fondamental comme on l'avait fait jusqu'alors,
j'ai reconnu : 1° que les longueurs des parties vibrantes
de la colonne d'air à partir de l'extrémité
ouverte des
tuyaux se trouvaient toujours conformes à la théorie
de
D. Bernouilli, c'est-à-dire que ces parties étaient
égales
aux longueurs d'onde correspondantes au ton des
tuyaux ; 2° que le diamètre du tuyau n'avait aucune
influence sur la longueur de ces subdivisions de la
colonne d'air, mais que la partie contiguë à l'em-
bouchure subissait, au contraire, un raccourcissement
d'autant plus grand que le diamètre du tuyau était
plus considérable.
« Cette
dernière circonstance, observée par Bernouilli
lui-même et par les physiciens qui ont étudié
la question
après lui, avait porté les théoriciens à
faire abstraction
de l'embouchure des tuyaux pour ne considérer que des
tubes complètement ouverts aux deux bouts, ou bien
entièrement fermés d'un seul côté.
De cette manière on
(1) Note de M. Cavaillé-Coll, lue à
l'Académie des sciences de Paris, le
23 janvier 1860.
|
mettait à peu près la théorie
d'accord avec l'expérience ;
mais ce genre de tubes sans embouchure ne pouvait rece-
voir aucune application dans la facture instrumentale.
« Toutefois, comme dans la pratique on ne peut pas
se contenter des spéculations isolées de la théorie,
il
était nécessaire de considérer les tuyaux
munis de
leurs embouchures usuelles et de chercher à mettre la
théorie d'accord avec les faits.
« Après quelques expériences sur des tuyaux
de bois
de différentes dimensions, je crus m'apercevoir que la
véritable longueur du tuyau était égale à
la longueur
de l'onde (correspondante à son intonation) diminuée
de
deux fois la profondeur intérieure du tuyau.
« Les observations que j'ai eu occasion de faire
depuis cette époque sont venues confirmer mes prévi-
sions. Voici quelles furent mes premières expériences
:
« Un tuyau de bois à base carrée donnant l'ut
2
(dit de 4 pieds), coupé en ton d'après le la
normal de
880 vibrations par seconde, ayant 0m08 de
profondeur
intérieure et pour longueur 1m13.
Le ton de ce tuyau
correspondant à 264 vibrations par seconde.
« Maintenant si nous supposons la vitesse du son à
la température moyenne de 15 degrés de 340 mètres
par seconde, l'onde sonore correspondante au tuyau
340m
précité sera de ------- =
1m288, et si nous retranchons
264Vib
de la longueur de l'onde trouvée deux fois la profondeur
du tuyau, c'est-à-dire 0m08 X 2 =
0m160, on aura,
pour la longueur calculée du tuyau, 1m128,
ce qui ne
|
donne qu'une différence de 0m002
sur la longueur
trouvée expérimentalement qui est de 1m130.
« L'ut grave
de 32 pieds de la pédale de flûte de
l'orgue de Saint-Denis avait été coupé à
la longueur de
9m566; sa profondeur est de 0m48.
Ce tuyau s'est
trouvé trop long d'après le diapason de 880 vibrations
par seconde, sur lequel cet orgue est accordé. Ce
résultat est venu encore confirmer l'hypothèse ci-dessus.
L'onde sonore de ce tuyau étant de
340m
------- =
10m30
33vib.
en diminuant le double de la profon-
deur, c'est-à-dire 0m48 X 2 = 0m96
ci................................................................
0m96,
il reste pour la longueur calculée du
tuyau ......................................................... 9m34
« Or, la différence de 0m226
en moins de la longueur
calculée à la longueur d'abord fixée s'est
trouvée justi-
fiée par l'ouverture qu'on a dû pratiquer à
l'extrémité
du tuyau pour l'accorder en sa place.
« D'après ces premières observations, je fus
natu-
rellement conduit à vérifier cette loi sur des tuyaux
de
dimensions les plus opposées, et l'expérience ayant
constamment confirmé mes prévisions, j'en ai conclu,
ainsi que je l'avais tout d'abord remarqué, que la lon-
gueur des tuyaux en bois est égale à la longueur
de
l'onde sonore diminuée de deux fois la profondeur du
même tuyau.
« Si nous désignons par
V la vitesse du son,
|
|
N le nombre de vibrations,
L la longueur du tuyau,
P la profondeur intérieure,
on aura, pour déterminer l'un de ces quatre éléments
qui
concourent à la détermination du ton.
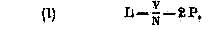
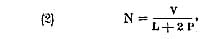
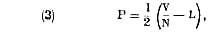
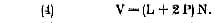
« Soit, en langage ordinaire :
« (1) La longueur du tuyau est égale au quotient
de
la vitesse du son par le nombre de vibrations diminué
de deux fois la profondeur.
« (2) Le nombre de vibrations est égal au quotient
de
la vitesse du son par la longueur du tuyau augmentée
de deux fois la profondeur.
« (3) La profondeur est égale à la moitié
du quotient
de la vitesse du son par le nombre de vibrations dimi-
nué de la longueur du tuyau.
« (4) Enfin la vitesse du son est égale au produit
de
la longueur du tuyau augmenté de deux fois la profon-
deur par le nombre de vibrations.
« Dans une autre série d'expériences sur des
tuyaux
cylindriques en métal, nous avons été à
même de
reconnaître que la loi qui s'applique aux tuyaux pris-
|
matiques en bois à base carrée régit
également les
tuyaux cylindriques.
« Nous devons toutefois faire remarquer qu'il ne faut
pas confondre la profondeur du tuyau avec son dia-
mètre, comme on pourrait le supposer par analogie avec
les tuyaux de bois à base rectangulaire. Dans ces der-
niers tuyaux, la profondeur est la même que la largeur
du côté perpendiculaire à la ligne de l'embouchure,
tandis que, dans les tuyaux cylindriques, la profondeur
est nécessairement plus petite que le diamètre.
L'apla-
tissement de la bouche, qui est habituellement du quart
de la circonférence du tuyau, forme une corde sous-
tendant un arc égal aux 3/4 de cette même circonfé-
rence. C'est ici la moyenne des perpendiculaires abais-
sées de cette corde sur l'arc opposé qui doit être
prise
pour la profondeur. Or, cette moyenne peut être repré-
sentée sans erreur sensible par les 5/6 du diamètre,
et
en remplaçant la valeur de P de notre formule par
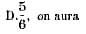
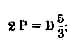
d'où il suit que, pour les tuyaux cylindriques, notre
formule sera
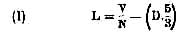
Soit enfin, en langage ordinaire : La longueur des
tuyaux cylindriques est égale au quotient de la vitesse
|
du son par le nombre de vibrations moins les 5/3 du
diamètre du tuyau.
« Plusieurs tableaux d'observations rapportés dans
ce
Mémoire viennent à l'appui de cette nouvelle théorie,
qui se trouve d'ailleurs confirmée par vingt années
d'application à la construction des grandes orgues que
j'ai exécutées depuis cette époque.
« La facilité des calculs de cette formule m'a permis
de mettre entre les mains de mes plus simples ouvriers
accordeurs des Tables et des règles où sont indiquées
les vraies longueurs d'ondes sonores, et au moyen des-
quelles ils peuvent, par une simple opération d'arith-
métique ou seulement de compas, déterminer directe-
ment et avec une exactitude rigoureuse la longueur
normale des tuyaux pour le son fondamental, la posi-
tion des nœuds de vibrations pour les sons harmoniques,
le prolongement des tuyaux à ouvertures latérales,
les
proportions de ces mêmes ouvertures, à l'effet de
régler
exactement l'accord et l'homogénéité des
sons. »
A. CAVAILLÉ-COLL.
|
 |
|
 Dimension
d'un tuyau
Dimension
d'un tuyau 