L'harmonie des sphères.

Propos extraits de l’excellent bouquin de Dominique Proust : “L’harmonie des sphères”, éditions Dervy-livres.

La clef fondamentale de l'ordre cosmique ne peut se trouver que dans une parfaite harmonie. Sans elle, la musique ne peut exister car l'harmonie est l'essence même des sons organisés. Forts de cette évidence, les Anciens tentent d'associer le plus étroitement possible le cosmos et la musique afin d'en montrer la parfaite symbiose.

Pythagore est probablement le premier à associer étroitement la musique et l'astronomie. Son intérêt pour la musique le pousse à définir la gamme qui porte son nom suivant deux principes : il n'existe que 7 intervalles entre les notes d'une gamme et la somme de ces intervalles est égale à 6 tons. Sa fascination pour les rapports numériques dans les harmonies musicales l'amène à tenter d'expliquer de la même manière les autres phénomènes de la nature, y compris le cosmos. Il utilise le mot "cosmos " pour désigner un univers ordonné et harmonieux. La dualité entre l'harmonie et l'astronomie fut ainsi établie par l'école Ionienne de Pythagore au 6e siècle avant notre ère.

La Terre est considérée comme un corps céleste isolé dans l'espace, au centre d'une sphère. Les planètes ne sont pas toutes à la même distance de la terre, posées sur des anneaux circulaires opaques. L'ordre des planètes fait appel à une hiérarchie fondée sur la mythologie, dans l'ordre : Terre - Lune - Vénus - Mercure - Soleil - Mars - Jupiter - Saturne - Fixes (étoiles). Une fois cet ordre établi, il faut donner des distances. La méthode va donc consister à deviner la loi des distances plutôt que de la calculer, suivant le principe de Pythagore.

Etant donné qu'il y a autant d'intervalles musicaux qu'il y a de planètes, il suffit de placer celles-ci suivant les rapports harmoniques. Les sept planètes sont comme les sept cordes d'une lyre. En fixant la valeur du ton comme étant égale à la distance Terre - Lune, les Pythagoriciens établissent ainsi la première échelle planétaire. D'après eux toutes les planètes, y compris le soleil et la lune, tournent autour de la terre à vitesse constante suivant des orbites obéissant aux mêmes rapports numériques que la gamme. Chacune d'elle produit un son correspondant au si pour Saturne, do pour Jupiter, ré pour Mars, mi pour le soleil, fa pour Mercure, sol pour Vénus et enfin la pour la Lune.

Cicéron (106 - 43 av JC) donne une description admise en son temps : L'univers est composé de neuf cercles ou plutôt de neuf globes qui se meuvent. La sphère extérieure est celle du Ciel, qui embrasse toutes les autres et sous laquelle sont fixées les étoiles. Plus bas roulent sept globes, entraînés par un mouvement contraire à celui du ciel.
Sur le premier cercle roule … Saturne ;
sur le second marche Jupiter , … ;
vient ensuite Mars, … ;
au dessous, occupant la moyenne région brille le Soleil, … .
Après lui viennent … Vénus et Mercure.
Enfin l'orbe inférieure est occupée par la Lune …

Boèce a repris la construction de Pythagore attribuant cette fois la note ré à la Lune (au lieu du la initial), à Mercure le do, et ainsi de suite : Lune ré, Mercure do, Vénus si, Soleil la, Mars sol, Jupiter fa, Saturne mi.
On retrouve une telle cosmologie dans les anciennes cultures orientales, en Inde et en Chine notamment.

Dans un fragment de musique grecque qui nous soit parvenu - l'hymne au soleil de Mesomède de Crète, 130 av JC - on se fait une idée de la musique antique : chaque note est émise seule, sans accompagnement (elle est dite homophone) et l'ambitus de la mélodie est faible. Les notes appartiennent à une suite bien définie de sons. On peut aussi par la musique expliquer l'ordre des jours de la semaine dont l'ordre apparemment arbitraire se réfère en fait à la gamme de Boèce.

En remplaçant chaque jour par sa note, la semaine se déroule suivant une série de quintes parallèles descendantes Lundi Lune ré,
Mardi Mars sol,
Mercredi Mercure do,
Jeudi Jupiter fa,
Vendredi Vénus si,
Samedi Saturne mi,
Dimanche Soleil la.

Jusqu'à la fin du Moyen Age la musique est enseignée avec les mathématiques, considérant que celles-ci comprennent :
- L'arithmétique,
- La musique,
- La géométrie,
- L'astronomie.
C'est " le quadrivium ". La conception même d'un lien entre les planètes et la musique ne peut avoir de sens que par une approche de l'acoustique.

Dans le domaine de la science des sons, les Grecs n'ont produit que deux traités majeurs : La division du canon, d'Euclide, et Les harmoniques, de Ptolémée.
Dans le second, les différentes théories musicales sont soigneusement analysées et comparées à l'harmonie des sphères, conformément aux théories pythagoriciennes. Ptolémée insiste particulièrement sur les relations entre certains mouvements des astres et différentes propriétés caractéristiques des sons, entre le tétracorde et le système solaire, entre les premiers nombres du système parfait et les premières sphères du monde, enfin entre les propriétés des planètes et celles des sons.

(Retour haut de page)

Censorin, astrologue romain, publie en 238 - De die natali - où il reprend les doctrines de Pythagore. On y trouve en particulier des distances astronomiques calculées en tons musicaux :
De la Terre à la Lune un ton
De la Lune à Mercure un demi ton
De Mercure à Vénus un demi ton
De Vénus au Soleil un ton et demi
Du Soleil à Mars un ton
De Mars à Jupiter un demi ton
De Jupiter à Saturne un demi ton
De Saturne aux fixes un demi ton
De la Terre au Soleil il y a trois tons et demi, soit une quinte, tandis que du Soleil aux fixes (étoiles) il n'y a que deux tons et demi, soit une quarte.
On retrouve cependant les six tons (une octave) pour aller de la Terre aux étoiles.

Au fur et à mesure que la conception de l'univers évolue en se perfectionnant, la musique aussi évolue.
Depuis la lyre d'Hermès à 4 cordes on avait vu apparaître la lyre de Terpandre dont les 7 cordes correspondaient à la jeune théorie pythagoricienne. Terpandre innove en matière d'écriture musicale et rythmique.
L'évolution continue lorsqu'une huitième corde est ajoutée, celle-ci attribuée au zodiaque car celui-ci lie le signe de naissance d'un individu au déroulement de son existence (c'est la date de conception chez les Babyloniens !).
La Terre elle-même devant être prise en compte, une neuvième corde voit le jour.

Cependant, pour pouvoir produire un son, la terre doit être mobile. Ainsi naît le premier modèle non anthropocentrique, dit modèle de Philolaos, où la terre n'occupe plus le centre du monde mais tourne en un jour autour d'un feu central autour duquel tourne également une anti-Terre qui nous est cachée, de même que le feu central puisque nous habitons sur la face tournée vers l'extérieur.

Sautons quelques siècles pour arriver au moyen age. Les neuf cordes de la lyre céleste augmentent jusqu'à 15 pour expliquer, au-delà des planètes, le Ciel, les Puissances, les Principautés, les Dominations, Trônes, Chérubins et autres Séraphins, pour aboutir à Dieu.
A l'autre extrémité il y a la terre qui, ayant retrouvé son immobilité au centre du monde, ne peut participer à l'harmonie générale et conserve le " silentium ".

Le musicographe grec Alypius utilise au 4e siècle le clavier de la cithare à 18 cordes pour établir un système de sphères célestes d'une extrême complexité.
Son contemporain Macrobius étend le système harmonique à 4 octaves et demi.

Tout au long du moyen age l'étude de l'harmonie est une partie intégrante des mathématiques. Anthropocentrisme et harmonie sont les principes avec lesquels l'église étend son autorité mais il convient aussi de célébrer les louanges du créateur par le chant. L'accord entre la théorie et la pratique est réalisé d'abord par la dénomination des notes ut … ré … mi … fa … sol … la … si (le " si " est arrivé plus tard !) et ensuite par l'introduction de la mesure au 12e siècle.

Le plain-chant est abandonné au 10e siècle au profit de l'organum consistant en l'exécution de la même mélodie par deux voix distantes d'une quarte ou d'une quinte. Ensuite vient le déchant, strict contrepoint note contre note, pour aboutir à la polyphonie à travers Machaut et Jannequin qui intégra même les bruits de la vie dans ses compositions.

L'hymne du 12e siècle " Naturalis concordia vocum cum planetis " est l'œuvre musicale la plus ancienne connue inspirée de l'harmonie des sphères. Il utilise une gamme planétaire de 2 octaves, la première consacrée aux astres et la seconde à la zoologie des bienheureux. Elle diffère de celle de Boèce :
Ciel fa,
Saturne mi,
Jupiter ré,
Mars do,
Soleil si,
Vénus la,
Mercure sol,
Lune fa,
Terre silentium !

(Retour haut de page)

A la Renaissance, cet équilibre idéal entre harmonie et physique devient intenable par la quantité de sphères et d'épicycles nécessaires pour expliquer les écarts et les nombreuses anomalies observées.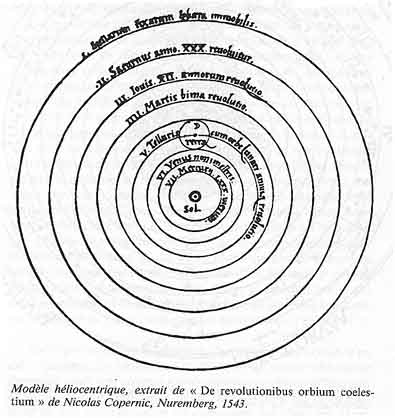
La vieille théorie de Philolaos qui faisait de la terre un astre mobile et sonore revient à la mode et est reprise en 1453 par Copernic (théorie de l'infini qui ne peut pas avoir de centre). La quête d'harmonie idéale correspond, sur le plan technologique, au développement de l'horloge, mère de toutes les machines. L'univers n'est qu'une vaste horloge mise en place par le Créateur … La musique est alors soumise aux impératifs rythmiques.

La révolution copernicienne entraîne la perte de notre anthropocentrisme : la Terre n'est plus qu'une planète comme les autres, tournant autour du Soleil.

Léonard de Vinci consacre un chapitre de ses travaux afin de savoir " si le frottement des cieux fait son ou non " et apporte des arguments pour réfuter la théorie.

Après la disparition de Copernic, Tycho-Brahé (1546 - 1601) construit le premier grand observatoire et cumule les observations qui sont scrupuleusement consignées. Il ne parvient pas à renoncer à la vision géocentrique de l'univers.

Johannes Kepler hérite de ses documents et énoncera les lois relatives au mouvement des planètes. Kepler attribue au soleil une fonction motrice, anime les planètes sur une orbite elliptique. Insatisfait, il recherche l'harmonie des sphères dans l'harmonie musicale, mode mathématique qui a le plus de chances d'être le fil conducteur vers la compréhension des intervalles planétaires. Dieu est architecte et géomètre mais il est aussi surtout musicien, donc il ne peut en être autrement ! Ce Dieu musicien doit donc attribuer à chaque planète une phrase musicale qui lui soit propre puisque, selon la tradition, chaque planète est vivante et douée d'une âme.

Selon Kepler la vitesse angulaire de chaque planète, dans son mouvement autour du Soleil, mesurée en secondes de degré par jour, fournit le nombre de vibrations de chaque son. Sur une orbite elliptique, la vitesse de chaque planète n'est pas constante et ce son décrit une phrase d'autant plus étendue que l'ellipse de l'orbite est allongée. La note fondamentale correspond à l'aphélie (distance maximale par rapport au Soleil).
Kepler arrive ainsi à obtenir les mélodies de base de chacune des planètes, les notes de la Terre pouvant être simplement mi, fa, mi, fa, … Autrement dit : " miseria, famina, miseria, famina … " (indéfiniment). Ce n'est pas là la vision d'un joyeux drille !
Le chant de Mercure est un soprano (sopraniste ? Mercure ?).
Celui de Vénus est un contralto et, en continuant ainsi à s'éloigner du Soleil, celui de Mars un ténor léger, et pour les géants Jupiter et Saturne, deux basses profondes.
Le résultat de ses travaux harmoniques " Harmonices mundi " est publié en 1619.
L'ambitus orbital de Mercure se compose d'une octave plus une tierce : do … do … mi.
Vénus répète inlassablement la même note : mi , mi , mi …
La Terre se limite à un demi ton : sol , lab , sol …
Mars donne une quinte : fa , sol , la , sib , do …
Jupiter se promène sur une tierce grave : si … ré,
ainsi que Saturne : fa … la

Quelques années plus tard Galilée s'attache également à établir un lien entre ses préoccupations astronomiques et ses recherches en matières musicales sous l'influence de son père, Vicenze Galilei (1520 - 1591). Organiste et compositeur, Vicenze eut Zarlino pour maître ; ses compositions inspirèrent Frescobaldi et Vivaldi.

Galilée

Marin Mersenne traduisit les ouvrages de Galilée et reprend ses travaux sur la vibration des cordes dans son " Harmonie universelle " en 1636. Son intérêt pour l'astronomie le pousse à y inclure des dessins de télescopes afin de réactualiser la question de l'harmonie des sphères.

Par la suite, si le divorce est définitivement consommé entre l'astronomie et l'harmonie, les planètes et les étoiles ont inspiré de nombreux musiciens et des témoignages de l'état des recherches se trouvent souvent traduit en musique. Pour citer quelques exemples, l'oratorio " la Création " de Joseph Haydn est inspiré des travaux de William Herschel qui a émis l'hypothèse d'une explosion originelle de l'univers et des théories d'Emmanuel Kant.
" Und es werde licht ! ".

La même démarche est formulée par Jean Fery Rebel dans " Les Elémens ", ne se résolvant pas, en 1737, à admettre la vision d'un monde organisé. (Mais n'y entend-t-on pas, en fait, le monde qui s'organise peu à peu ?)

(Retour haut de page)

Zodiaque et instruments de musique.

Les trajectoires apparentes des planètes ont la particularité de traverser toujours les mêmes constellations. Celles-ci traditionnellement au nombre de douze forment le zodiaque En réalité, il conviendrait d'en ajouter une treizième, Ophiuchus (ou serpentaire) mais l'évocation astrologique du chiffre 13 fut de nature à effrayer suffisamment Ptolémée qui préféra oublier cette dernière constellation.

La tradition a associé douze instruments de musique à chaque constellation. Sans attendre la Renaissance qui marque l'apogée de l'influence astrale sur l'iconographie musicale, de nombreux indices révèlent les liens puissants unissant le zodiaque et les instruments de musique.
La collégiale de Saint Bonnet le Château (près de Saint Etienne) nous en fournit un exemple. Les voûtes et les murs de la crypte sont décorés de fresques représentant, par leurs signes symboliques, les douze constellations du zodiaque. A chacune d'elle est associé un instrument de musique ou un ange musicien.
Au Verseau correspond le luth,
Aux Poissons, la mandore,
Au Bélier, le psaltérion,
Au Taureau, le clavicorde
Aux Gémeaux, la cornemuse,
Au Cancer, le carillon,
Au Lion, le cornet droit (cornetto dolce)
A la Vierge, le cornet gauche (cornet à bouquin)
A la Balance, l'orgue,
Au Scorpion, la harpe,
Au Sagittaire, la gigue (viole de gambe),
Et au Capricorne, la vièle.
L'artiste anonyme a concilié la musique avec le ciel d'hiver. Il harmonise le zodiaque afin que le chant des planètes soit accompagné d'instruments pendant leur ronde cosmique. Ces fresques cachent certainement d'étonnants rébus.

(Retour haut de page)

Pythagore et les principes de l'acoustique (d'après Boèce)

Sans plus tenir compte des appréciations fournies par des oreilles, Pythagore décida de n'employer que des rapports mathématiques pour la division de la règle des sons. Il cherchait de quelle manière il apprendrait les divisions fixes et constantes des rapports harmoniques quand, passant devant un atelier de forgerons, il entendit que les marteaux résonnaient en tirant une sorte d'accord. Il pensa que la diversité des sons provenaient des forces respectives de ceux qui frappaient. Il leur demanda d'échanger leurs marteaux mais les mêmes sons accompagnaient les marteaux une fois échangés.
Il examina alors le poids des marteaux qui étaient au nombre de cinq.
Ceux donnant l'accord de diapason (octave) étaient d'un poids double l'un par rapport à l'autre.
Celui qui était double de l'autre comportait les 4/3 d'un troisième et donnait le Diatessaron (quarte).
Mais par rapport à un autre avec lequel il formait l'accord de Diapente (quinte), il trouve pour ce marteau la valeur de poids de 3/2.
Les deux marteaux qui avaient les rapports 4/3 et 3/2, pesés exactement, gardèrent l'un par rapport à l'autre le rapport de 9/8 et donnaient entre eux la Sesquioctave (ton).
Quant au cinquième marteau qui était en désaccord avec tous, on le laissa tomber.

Pythagore fut ainsi le premier à trouver selon quel rapport chaque accord des sons entre eux était uni.
De retour chez lui, Pythagore examina si la raison des accords consistait toute en ces proportions :
En adaptant à des cordes égales des poids de valeurs différentes dans les mêmes proportions,
En variant la longueur de cordes auxquelles étaient attachés des poids identiques,
En établissant des chalumeaux de longueurs différentes suivant les mêmes proportions.
Ainsi, il en acquit la certitude et énonça la règle qui permet d'obtenir les rapports harmoniques.

Propos extraits de l’excellent bouquin de Dominique Proust : “L’harmonie des sphères”, éditions Dervy-livres.
(Sans son autorisation, mais c'est un copain !)

(Retour haut de page)

Harmonie

L'harmonie est le résultat d'une codification stricte de la gamme à laquelle notre oreille occidentale s'est progressivement entrainé.

La musique occidentale respecte les canons absolus des rapports de sons par multiple de 2. Le " la " 440 admet le " la " 220 à l'octave inférieure et le " la " 880 à l'octave supérieure. Comme la gamme comporte 12 demi-tons, le rapport de fréquence entre deux notes séparées d'un demi-ton respecte l'échelle logarithmique établie et vaut - racine douzième de 2 - La gamme tempérée théorique est bâtie sur ce principe.
Théorique parce que l'expérience montre que l'accord d'un instrument sur ce principe sonne tout à fait faux !
L'explication en est simple : racine douzième de 2 appartient à la famille des " irrationnels ". Les nombres irrationnels ont une infinité de décimales et, les négliger dans un calcul, revient à introduire une erreur systématique qui peut - comme en musique - se cumuler.

Mais on fait alors appel à la loi de Bode qui veut qu'on puisse distinguer une même mélodie quelle que soit la gamme dans laquelle elle est restituée. Seule l'harmonie en prend un coup !

Pythagore avait défini sa gamme différemment. En partant d'une note de base, par exemple le " do ", il multiplia sa fréquence par 3/2 afin de définir sa quinte supérieure " sol " et répéta cette opération pour construire des suites de quintes " ré - la - mi - si ". Il réalisa ce calcul après avoir observé que la longueur d'une corde donnant la quinte d'un son était égale aux 2/3 de celle fournissant son fondamental.
Procéder ainsi, c'est " ignorer " les octaves qui sont alors trop grandes d'une valeur d'un neuvième de ton. Mais, comme les lyres n'avaient pas plus de 7 cordes, cela n'avait pas d'importance ! De plus, sur le plan philosophique, l'idée d'infinité de la gamme en spirale est assez satisfaisante. C'est plus gênant maintenant pour un piano où apparaît une différence d'un demi-ton au bout de 4 octaves.

(Retour haut de page)