Traité de l'Orgue de Marin Mersenne

PROPOSITION XII. Déterminer si l'on peut faire un Orgue qui ait tous ses tuyaux de même hauteur , c'est à dire si la différence de leur seule largeur peut faire l'étendue des quatre octaves qui sont ordinairement sur l'Orgue : & montrer en quelle raison doivent être leurs largeurs pour faire de tels sons , & tels intervalles que l'on voudra.

Cette proposition est très remarquable , d'autant que plusieurs croient que si l'on fait un tuyau deux fois plus large , qu'il descendra aussi bas que lors qu'il est deux fois aussi long parce qu'il est de même contenance. Si on les remplit tous deux d'air ou d'eau ils en tiendront autant l'un que l'autre.
D'où il s'ensuivrait que le tuyau double en largeur, ou grosseur, descendrait d'une octave comme le tuyau qui est double en longueur de sorte que la raison des intervalles harmoniques suivraient celle des largeurs, ce qui est contraire à l'expérience et à la vérité.

J'ai fait faire exprès plusieurs tuyaux de même hauteur dont les diamètres de la base sont en même proportion que les nombres 1, 2, 4, 8 et 16 .
J'ai toujours remarqué que celui qui a son diamètre double descend seulement d'une tierce mineure plus bas que celui qui est sous-double en diamètre, excepté le plus délié d'entre tous, étant sous-double de celui qui le suit immédiatement, monte seulement d'un ton.

Les tuyaux dont je me suis servi ont tous 1/2 pied du Roi. Le diamètre de la base du plus délié (le plus fin) a seulement 3 lignes, le second a 1/2 pouce ou 6 lignes, car il est double du précédent. Le troisième a 1 pouce, le quatrième en a 2, et le cinquième en a un peu plus de 4 de sorte que les diamètres de ces cinq tuyaux suivent toujours la progression géométrique de deux à un, suivant les nombres précédents. Le diamètre du plus gros est sexdécuple du plus délié et sa capacité est en même raison avec du plus délié comme 256 à 1. (DGW : Ceci corrige ce qu'il dit à la première ligne).
Le moindre ne monte qu'un ton plus haut que le second dont le diamètre est double.
Le troisième qui a son diamètre double du second descend d'une tierce mineure plus bas que le second et, conséquemment, fait la quarte avec le premier.
Le quatrième descend d'une tierce mineure plus bas que le troisième, et par conséquent il fait le triton avec le second et la quinte superflue avec le premier.
Le cinquième descend encore plus bas que le quatrième d'une tierce mineure, de sorte qu'il fait seulement la septième majeure avec le plus délié dont le diamètre est 16 fois moindre, quoique si l'on pousse peu de vent dedans ou qu'on lui fasse une bouche un peu basse, il arrive à faire l'octave. En sa proportion, il faudrait l'augmenter de 2 pouces en diamètre pour faire l'octave juste, afin que son diamètre fut d'1/2 pied du Roi, c'est à dire 24 fois plus grand que celui du plus délié.
Les notes qui suivent montrent le son de chaque tuyau pour ceux qui n'entendent la raison des sons que par les notes.

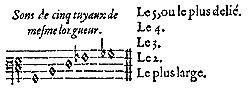Il est donc certain que la largeur des tuyaux ne peut compenser leur longueur puis qu'il n'est pas quasi possible de descendre ou monter jusqu'à l'octave avec des tuyaux de même hauteur. De plus, le plus délié qui a une longueur octuple de sa largeur ne peut quasi parler, ce qui arrive sensiblement au plus gros qui a un diamètre de 4 pouces pour une longueur de 6 pouces et qui a beaucoup de peine à sonner. On peut donc considérer que le tuyau le plus délié et le plus gros tiennent les deux souveraines extrémités et que l'octave borne la capacité de leurs largeurs et de leurs diamètres.

Corollaire.

Les deux premiers tuyaux les plus déliés ne gardent pas les raisons des plus gros entre leurs sons puis que le second étant double du premier ne descend que d'un ton et non d'une tierce mineure. Il faudrait en trouver la raison.

Après avoir expérimenté ce qui appartient à la largeur des tuyaux, il faut voir ce qui arrive à leurs différentes longueur afin que nous considérions ces cylindres concaves en toutes sortes de façons.