Traité de l'Orgue de Marin Mersenne

PROPOSITION XIV. Expliquer la raison que les tuyaux doivent avoir entre leurs longueurs , & leurs largeurs pour faire tous les degrés d'une ou plusieurs Octaves : & donner un Diapason très juste .

L'expérience nous a fait voir que les tuyaux doivent être de différentes longueurs et grosseurs pour faire tous les sons de l'Orgue. Il faut joindre ces deux dimensions ensemble afin d'avoir des sons qui soient proportionnés tant en leur aigu qu'en leur douceur et leur harmonie.

J'ai expérimenté que quand les longueurs de deux tuyaux sont en raison double, il ne suffit pas que leur largeur soit de même raison que la diagonale est au côté du carré, laquelle est la moitié de la raison double, parce que lors que cela arrive, le plus long ne fait pas l'octave.
Les diamètres des tuyaux doivent être en raison triple de la raison des intervalles, qui représentent les racines. La longueur des tuyaux est comme la raison double de celle desdits intervalles qui représentent la surface cylindrique des tuyaux

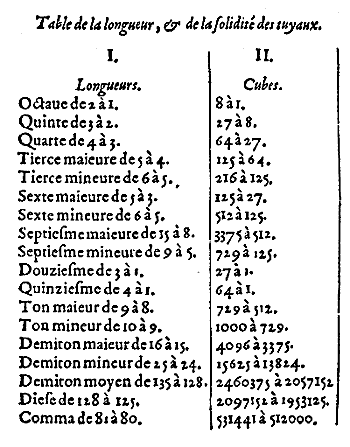
Il est aisé de supputer les cubes de tous les tuyaux et il faut seulement tripler les termes radicaux des raisons de chaque intervalle, comme a fait le sieur Cornu dans la table qui suit dont la première colonne représente la longueur, et conséquemment la largeur, de chaque tuyau, et la seconde représente la solidité, c'est à dire la capacité de leur vide. (Le volume du solide).

Il est aisé de trouver les bases et les surfaces des mêmes tuyaux puis qu'elles sont moyennes proportionnelles entre les simples termes des intervalles et leur cubes, c'est à dire qu'elles suivent les carrés.

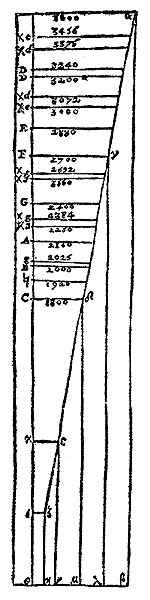
A quoi j'ajoute le Diapason des Orgues en faveur des Facteurs afin qu'il n'y ait nul artisan qui ne puisse comprendre aisément ce livre. Je le commence par C sol ut fa. On peut aussi le commencer par F ut fa ou par telle autre lettre que l'on voudra.
La ligne entière (verticale) représente le plus grand tuyau qui sert de fondement à tous les autres. Bien que cette ligne n'ait qu'un demi pied de long, on aura le tuyau de 32 ou 16 pieds si on le redouble 64 ou 32 fois.
Le second tuyau qui fait l'octave a 1/4 de pied et se prend depuis le second C jusqu'à . Il faut remarquer que la mesure de chaque tuyau se trouve d'autant plus aisément qu'il fait une meilleure consonance et un plus excellent accord avec le premier, De là vient que l'on trouve le tuyau qui monte à l'octave plus aisément que nul autre.
En second lieu on trouve le tuyau qui fait la quinte, ou G ré sol, en divisant la ligne entière en trois parties égales, dont les deux donnent G ré sol de sorte qu'il faut laisser un tiers de la ligne depuis le premier C jusqu'au G, comme il faut laisser 1/4 de la même ligne pour avoir le tuyau F qui fait la quarte.
Après il faut laisser 1/5 partie pour avoir l'E mi la qui fait la tierce majeure. 1/6 pour avoir la feinte supérieure d'E mi la (Mi b ?) qui fait la tierce mineure contre le premier C. Mais pour avoir la sixte mineure, c'est à dire le tuyau de la feinte supérieure d'A mi la ré, il faut laisser 3/8 de la ligne entière divisée en huit parties. 3/5 de la ligne divisée en cinq parties pour avoir le tuyau d'A mi la ré, ou la sixte majeure.

Tous les autres tuyaux se trouvent semblablement par le moyen des consonances, car le B fa se rencontre en divisant le tuyau F en quatre parties, dont les trois donnent le tuyau B qui fait la quarte avec F. Et si l'on divise le tuyau G en cinq parties égales, les quatre donnent le mi b qui fait la tierce majeure avec le G.
Il est aisé de trouver toutes les autres feintes par les mêmes consonances car si l'on divise E en cinq parties égales et que l'on ajoute une de ces parties depuis E vers C, on aura la feinte supérieure du premier C, laquelle fait la tierce mineure avec E.
Si l'on encore avoir la tierce majeure en haut contre A, il faut diviser A en cinq parties dont les quatre donnent une nouvelle feinte en haut (F# ?) et huit semblables parties prises sur la ligne entière la donnent en bas.
Nous n'avons pas encore trouvé le tuyau D la ré sol qui est la seconde diatonique laquelle on peut trouver de plusieurs manières. Si on divise le tuyau A en deux parties et que l'on ajoute l'une de ces parties vers le premier C, on aura le tuyau D. On le trouve aussi en divisant F en cinq parties égales auxquelles, si l'on en ajoute encore une, on aura le même D. On le trouve encore en divisant la ligne entière en 9 ou 10 parties, car l'une de ces parties étant retranchée l'on a l'un ou l'autre des D la ré sol qui font le ton majeur ou le mineur avec C.
Finalement l'on aura la feinte de F si l'on divise D en six parties dont les 5 donneront ladite feinte, qui fait la tierce majeure en bas contre D.
Conséquemment on a les treize touches du clavier ordinaire et les treize tuyaux du registre, ou d'un jeu d'1/2 pied ouvert ou bouché.

Je laisse plusieurs autres manières dont on peut user par le moyen des consonances pour trouver les mêmes tuyaux afin d'en expliquer une seconde qui commence par les moindres intervalles alors que la première a commencé par les plus grands.
On trouve premièrement la première feinte de C en divisant ledit C, c'est à dire le plus grand tuyau ou la plus grande ligne, en 25 parties égales dont on en retranche une pour avoir ladite feinte.
Si l'on veut la seconde feinte de C, laquelle est souvent nécessaire pour faire des consonances justes, il faut diviser C en 16 parties et en retrancher une pour marquer la seconde feinte qui fait la seconde mineure ou le demi ton majeur avec ledit C, contre lequel la première fait le demi ton mineur.
L'on a le tuyau D en divisant C en dix parties dont on en retranche une car les 9/10 donnent le premier D, qui fait le ton mineur contre D. Mais il faut diviser C en neuf parties et en retrancher une pour avoir le second D qui est éloigné de l'autre d'un comma.
Si l'on veut avoir deux feintes de D comme l'on a deux feintes de C, il faut diviser ce second D comme l'on a divisé C, à savoir 25 parties pour avoir la feinte de 24, et en 16 pour avoir celle de 15.
Et puis il faut diviser le premier C en neuf parties ou le second en dix, pour avoir le tuyau E, en retranchant la 1/9 ou la 1/10 partie.
Et l'E mi la divisé en seize parties, dont on en retranche une, donne 15 pour F, duquel on aura les deux feinte en le divisant comme C en 24 ou en 16, car 24 donnera sa première feinte et 15 sa seconde. Il donnera aussi 8 parties pour le G lorsqu'il aura été divisé en 9 et le G étant divisé comme le C ou le D donnera ses deux feintes, demi ton majeur et mineur, et le tuyau A contre lequel il fait le ton mineur.
L'A étant divisé en 16 parties, les 15 donnent le B et s'il est divisé en 9, les 8 donnent le b carre, lequel étant divisé en 16 parties, les 15 donnent le dernier tuyau C, qui fait l'octave en haut contre le premier C.

Il appert que les Facteurs n'ont pas besoin d'une plus grande connaissance pour faire leur Diapason et leurs tuyaux très justes, quoi que tous les tuyaux dont j'ai parlé ne soient pas suffisants pour donner toutes les consonances justes contre chaque marche, et que l'on puisse encore désirer quelques feintes pour ce sujet. C'est pourquoi j'ajoute un autre Diapason si universel que l'on n'y peut rien désirer de plus si l'on ne veut passer jusqu'à l'infini.

La figure précédente est un peu différente de la dernière description que j'ai faite du dernier Diapason ou de la dernière description que j'ai expliqué car les deux feintes qui sont entre F et G ne diffèrent que d'un comma, et le B est double, comme le D.
Quant au nombre 3600, qui signifie que le plus grand tuyau étant divisé en autant de parties, les autres tuyaux ont celles qui restent. Il est le moindre de ceux qui peuvent représenter les 19 tuyaux, ou les 19 sons de l'octave, qui a toutes ses consonances parfaites et où j'ai fait voir l'usage de ce diapason.