Traité de l'Orgue de Marin Mersenne

PROPOSITION XXII. Expliquer la science du clavier des Orgues , & combien il doit avoir de marches pour comprendre la perfection du genre Diatonic* , Chromatic* & Enharmonic*.

* (Sic)

La connaissance du clavier des Orgues dépend de la suite des ses degré car il faut savoir la raison des intervalles qui se rencontrent dans l'octave pour toucher les marches qui font les consonances et les dissonances, afin d'exprimer le dessein que l'on a, et la dignité du sujet.

Le clavier ordinaire tant tant des grandes Orgues que des Cabinets a treize marches sur chaque octave (de C à c) et n'est nullement différent de celui des Épinettes. Il faut aussi connaître toutes les variétés des chants et des compositions qui se peuvent faire dessus, et tous les mouvements, les martèlements, les tremblements,les passages, les échos et les autres gentillesses dont les Orgues sont capables.
Les claviers sont quelques fois doubles ou triples dans les grands buffets d'Orgue. Mais il suffit d'en connaître un pour juger des autres parce qu'ils sont tous semblables, encore que l'on puisse ajouter quelque nombre de marches aux uns plus qu'aux autres.

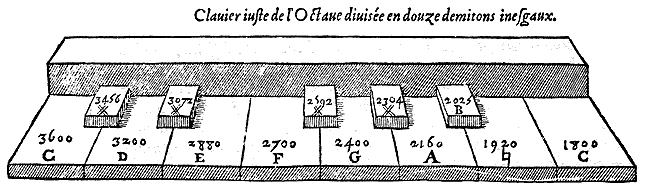
Le premier clavier qui suit, qui a treize marches sur chaque octave, commence en C sol ut fa, bien que l'on peut le commencer par telle autre lettre que l'on voudra et que le son de chaque tuyau soit indifférent pour figurer le son de toute forme de lettre. Les nombres qui sont sur ce clavier représentent les justes raisons de chaque intervalle afin que l'on sache la proportion de tous les tuyaux à la seule vue de ce clavier. Le premier, à savoir 3600, représente le premier C sol ut fa qui est éloigné de la feinte 3456 d'un demi ton mineur, et cette feinte est éloignée du D la ré sol d'un demi ton moyen afin qu'il y ait un ton majeur entre C et D.
D est distant de la feinte qui suit d'un demi ton mineur, et cette feinte 3072 est éloignée d'un demi ton majeur d' E mi la. Il s'ensuit qu'il y a un ton maxime ou superflu d' E à F ut fa, ( je suppose qu'il veut plutôt dire "jusqu'à", c'est à dire de D# à F !) c'est à dire un ton composé de deux demi tons majeurs et que F n'a point de tierce mineure en bas, ni C en haut.
De F ut fa à la feinte 2592 (F#) il n'y a qu'un demi ton mineur et par conséquent un ton mineur de E à F#. C'est pourquoi D ne peut avoir de tierce majeure en haut. De cette feinte à G ré sol il y a un demi ton moyen d'où il arrive qu' E mi la fait la tierce mineure contre G qui fait la quarte et la quinte juste contre C et D.
De G ré sol à la feinte 2304 (G#), il y a un demi ton mineur, et de cette feinte à A mi la ré, un demi ton majeur. Donc C a la sixte majeure en haut, D à la quinte, E la tierce majeure, et A (F ?) la tierce mineure. Mais C n'a point de sixte mineure comme a D contre B duquel il y a un demi ton moyen jusqu'à B carre (B carré = Si naturel, que les Germaniques représentent d'ailleurs par h, c'est à dire pas loin du signe représentant le bécarre). Le B n'a pas de sixte ni de tierce mineure en bas. Il est aisé d'en conclure que le clavier de treize marches sur l'octave ne peut avoir toutes les consonances justes, quelque disposition qu'on leur puisse donner.

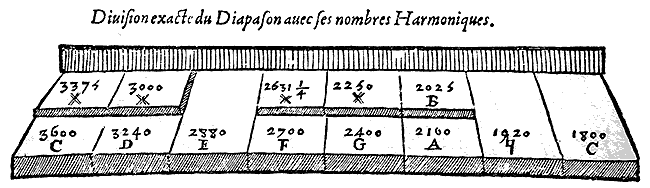
Si l'on met le demi ton majeur depuis C jusqu'à la première feinte au lieu du mineur, et qu'elle soit distante d'un demi ton mineur du D, afin qu'il n'y ait qu'un ton mineur de C à D, et qu'il y ait un demi ton maxime à # 3000, on aura des consonances qui ne se trouvent pas dans le clavier précédent, mais il en manquera plusieurs dans ce second qui se rencontrent dans le premier. Ainsi le D de celui-ci n'a pas la tierce majeure en haut, pas plus que l'autre, d'autant que le feinte 2631 de G est éloignée de F d'un demi ton majeur. Il y a un demi ton moyen de cette feinte à G et un demi ton majeur de G à la feinte de A de sorte que E de ce clavier n'a pas la tierce majeure en haut comme l'autre. Il est aisé de comprendre les autre degrés des nombres de ce second clavier. Mais il n'est pas possible que ces treize degrés fassent les consonances justes, nécessaires aux Organistes qui ont besoin de les trouver toutes contre chaque lettre Diatonique.

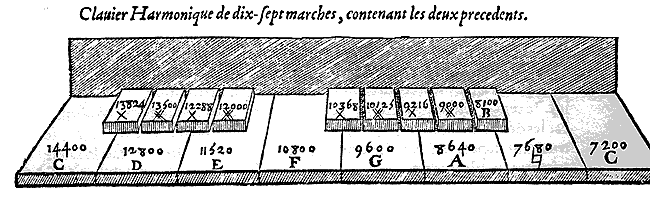
C'est pourquoi il faut user d'un clavier qui contienne les deux précédents, ce qui n'est possible que s'il a 17 degrés dans l'octave et s'il est disposé comme celui qui suit dans lequel il manque encore quelques marches. B carre a la tierce majeure en haut, F a la mineure, la feinte #F a la majeure, ce qui n'arrive pas aux claviers ordinaires car le D ne peut avoir la quarte juste en bas alors qu'il a la quinte juste en haut (? pourtant, l'octave est juste ?). Ceci est pourtant nécessaire pour la perfection de l'harmonie et des Orgues car le tempérament dont on use pour trouver ces consonances ne peut contenter ceux qui veulent entendre la perfection des proportions dans les accords et dans l'harmonie.

C'est pourquoi je veux ajouter ici un clavier avec les marches nécessaires pour faire toutes les consonances dans leur justesse, bien que les 19 marches de son octave soient, ce semble, plus difficiles à toucher que les 13 des autres claviers. Néanmoins la perfection de l'harmonie et la facilité qu'il y a à accorder les Orgues, qui usent de ce quatrième clavier, récompense abondamment la difficulté du toucher, que les Organistes pourront surmonter en l'espace de huit jours ou dans fort peu de temps.

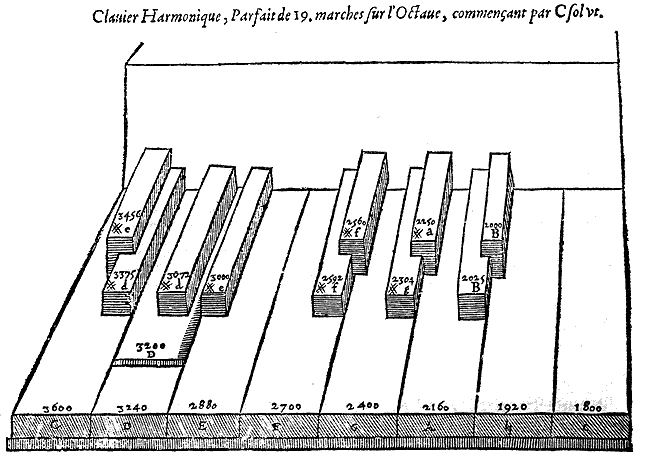
Ce qu'il y a de plus notable dans ce quatrième clavier consiste en ce qu'il a deux D qui ne sont comptés que pour un seul D la ré sol d'autant qu'il ne sont éloignés que d'un comma.
Il n'est nullement nécessaire d'expliquer les degrés de cette octave, ni les distances ou intervalles qui sont d'une marche à l'autre, ni l'usage de ce clavier.
Je répète seulement que ce clavier contient les trois genres de Musique car les deux dièses enharmoniques, à savoir majeur et mineur, se trouvent depuis le C sol ut fa jusqu'à la troisième marche qui fait le dièse mineur avec la seconde comme la seconde fait le majeur avec la troisième (?) et ces deux dièses font le demi ton majeur. Mais le diton qui doit achever le tétracorde enharmonique est depuis la troisième marche jusqu'à la neuvième, c'est à dire jusqu'à E (?! Je n'en compte que 8. Ne serait-ce pas plutôt F ? En effet, il y a 2 tons de do# à fa).
Il est aisé de trouver les autres tétracordes de ce genre.
Quant aux degrés chromatiques, ils sont déjà sur les claviers ordinaires pais pas avec une telle perfection que sur celui-ci dans lequel le demi ton majeur est de C à la troisième touche (3375) et le mineur de la troisième à la quatrième. Mais la tierce mineure qui achèvera le tétracorde chromatique est de la quatrième touche à la neuvième, c'est à dire de D à F.
Enfin le genre diatonique y est en sa perfection car il y a un ton mineur de C au premier D, un ton majeur de ce D à l' E, de sorte que le demi ton majeur qui est d' E à F achève la quarte diatonique.

Mais parce que ce clavier peut commencer par une autre lettre que C et qu'il peut avoir quelques unes de ses marches autrement disposées, je l'ajoute encore ici en le commençant par F ut fa, c'est à dire une quarte plus haut ou une quinte plus bas.

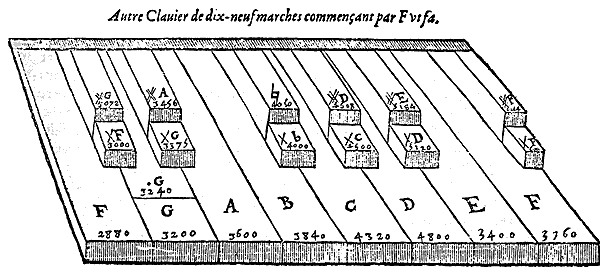
On peut trouver deux autres espèces de tétracorde chromatique dans ces deux claviers, à savoir celui qui est composé du demi ton majeur, du moyen et de la tierce mineure fausse, celui qui est composé du demi ton moyen, du mineur et de la tierce mineure superflue qui surpasse la tierce mineure juste d'un comma et dont la tierce diminuée est moindre que la juste d'un comma majeur, J'ai expliqué tous ces degrés et j'en parlerai encore dans la proposition qui suit