Traité de l'Orgue de Marin Mersenne

PROPOSITION XXIII. Déterminer s'il est expédient de changer les claviers ordinaires des Orgues , & en quoi consiste l'usage du clavier parfait : où l'on voit l'explication du clavier de vingt-sept & de trente-deux marches.

Si l'observation des lois dépendait des intervalles de la Musique et s'ils étaient cause du changement des mœurs et des bonnes coutumes, comme il semble que les Anciens ont cru, on aurait sujet de douter s'il est expédient ou s'il est permis d'ajouter de nouvelles marches aux claviers des Orgues, puis que nous lisons qu'ils ont banni ceux qui ajoutaient de nouvelles cordes aux instruments. Mais l'expérience ne nous a pas encore fait voir que cette augmentation de cordes ou de marches soit préjudiciable à l'état, ou aux mœurs, et les Facteurs ont déjà ajouté plusieurs feintes aux claviers, lesquelles sont hors des degrés de l'échelle harmonique de Guy Aretin, car ils divisent l'octave en douze demi tons par le moyen de treize marches.

Quoi qu'il en soit, le changement de pis en mieux par lequel on gagne beaucoup, comme est celui des claviers ordinaires, ne doit pas être blâmé si l'on ne blâme ceux qui, pour embellir les chants et les airs à une ou plusieurs voix, ajoutent plusieurs b mol et autres accidents qui sont hors des lettres ordinaires de la Musique.
Les claviers augmentés ne doivent pas être estimés extraordinaires puisqu'ils ne font autre chose que ce que font les voix et qu'ils mettent seulement l'harmonie dans la perfection où l'esprit et l'oreille la désirent.
Il est certain que ces claviers doivent être préférés aux anciens puisqu'ils contiennent une plus grande multitude de consonances et d'autres intervalles dans leur justesse et qu'ils imitent la voix plus parfaitement. Il n'importe nullement que la difficulté de les toucher soit plus grande d'autant qu'il ne faut pas plaindre la peine ni fuir le travail qui conduit à la perfection.

C'est pourquoi je mets une table vis à vis, qui contient ses 27 lettres, ou caractères, tant en biais suivant la diagonale du carré, que perpendiculairement suivant la base du même carré. De là vient que chaque colonne est divisée en 27 autres petits carrés de sorte que le grand carré contient 759 cellules. Celles qui ont les caractères ou les signes des sept planètes qui signifient les sept consonances, et les autres ont des nombres qui signifient les degrés et les intervalles dissonants.

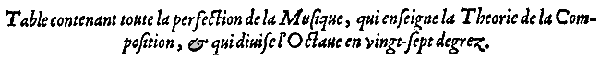
Le tableau montre les 27 degrés. La première colonne correspond au système parfait de Salinas qui commence sur E, comme le carré. Sur la deuxième colonne, la même chose transposé en C, comme le clavier. Comme dans le dessin du clavier ci dessous, deux notes n'ont pas de nombre car elles n'existent pas dans le Diapason de Salinas qui n'a que 25 degrés. Il s'agit du deuxième E et du deuxième G

.

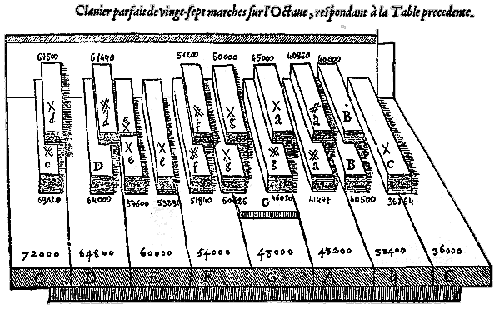
Ce clavier commence par C sol ut fa afin que l'usage en soit plus aisé. Je mets les lettres et les nombres harmoniques sur les marches afin que l'imagination ne travaille nullement et que les mains la suivent aussi aisément que l'ombre suit le corps
L'utilité que l'on peut tirer de ce clavier est fort grande car il fait voir très exactement les intervalles des trois genres de musique. Le clavier est divisé en trois sortes de marches : les plus basses montrent les degrés diatoniques, les secondes en montant signifient les degrés ou les marches chromatiques et les troisièmes font voir les degrés enharmoniques.

Corollaire I

L'on peut commencer les claviers par G ré sol ut, comme a fait Aretin dans la main harmonique, ou par D la ré sol comme l'a fait Glaréan, après les Grecs, qui commencent leur système par le proflambanomène, ou encore par F ut fa comme on l'a fait autrefois sur l'Orgue; ou par E mi la comme les plus anciens musiciens qui commencent leur tétracorde par Hypare hypaton et par l'intervalle du demi ton; car la Nature n'a point prescrit de bornes au commencement de la musique et l'art n'a point d'autre autorité que celle que lui donne l'esprit de l'homme, ou la coutume.

Corollaire II

Il est aisé de savoir les consonances qui sont ajoutées à ce clavier dont celui de Salinas est privé. Mais puiqu'elles ne peuvent se trouver juste sur l'un ni sur l'autre sans la relation du comma, il faut encore ajouter cinq marches afin d'avoir 32 degrés sur chaque octave qui répondent à la huit, neuf et dixième colonne de la table des diapasons que j'ai expliqué dans la quinzième et seizième proposition de ce livre.
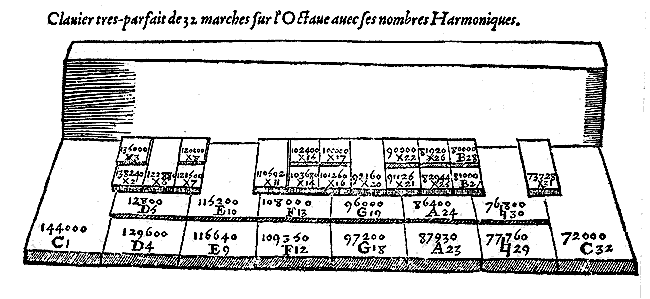
Je mets donc encore ce clavier de 32 marches qui font toutes les consonances. Les marches ajoutées sont aisées à remarquer, à savoir le second E, le second F, le second G, le second A et le second B carre qui, toutes, font l'intervalle du comma avec celle qui les précèdent. Les nombres qui sont à côté des marches signifie seulement le rang des marches que les Facteurs peuvent disposer comme il leur plaira.

(Vous en connaissez, vous, qui ont fait des sommiers de 128 gravures et se sont astreints à accorder 32 tuyaux par octave de chaque jeu ?).