Traité de l'Orgue de
Marin Mersenne.

PROPOSITION XXXVIII. Expliquer une méthode universelle pour le Diapason des instruments , & pour la division du Monocorde , & du manche des instruments à corde : où l'on voit une nouvelle Théorie de la Musique.

Monsieur Boulliau, l'un des plus excellent Astronome de notre siècle, m'a donné une table harmonique qui mérite d'être insérée dans ce traité parce qu'elle contient toute la Théorie de la Musique et qu'elle doit être considérée de tous ceux qui aiment l'Harmonie.
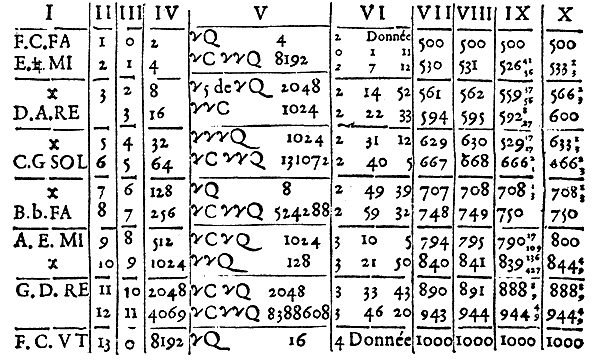
Elle est composée de dix colonnes dont la première contient les notes ordinaires de Guy Aretin, avec les dièses entre eux, qui signifient les demi tons.
La deuxième contient les nombres qui signifient la progression géométrique.
Les nombres de la troisième montrent l'ordre des onze moyennes proportionnelles.
Ceux de la quatrième sont en proportion double géométrique.
Ceux de la cinquième signifient les puissances des moyennes proportionnelles avec les signes radicaux pour l'extraction des racines.
La sixième colonne contient lesdites racines si précisément que les fractions qui suivent les nombres entiers vont jusqu'aux premiers et secondes minutes.
Les nombres de la septième et de la huitième montrent la longueur des tuyaux et des cordes qui font les treize sons de l'octave divisée en douze demi tons égaux si précisément qu'il ne leur manque pas l'unité car ceux de la septième sont trop petits et ceux de la huitième sont trop grands, ce qui revient à la table que j'ai mis pour le même sujet dans la quatorzième proposition du premier livre des Instruments et à celle de la neuvième proposition du quatrième.
Les nombres de la neuvième colonne signifient la longueur des cordes suivant la Théorie de Pythagore, laquelle a duré jusqu'à Glaréan, car il fait tous les tons majeurs qu'il divise en apotome et en dièse.
La dixième suit la Théorie de Ptolémée qui met le ton majeur et le mineur et qui divise arithmétiquement les tons mineurs et les majeurs.

Où il remarque en premier lieu que la progression harmonique est tellement composée de la Géométrique et de l'Arithmétique, qu'elle vient de deux progressions géométriques jointes ensemble sous la raison double et suivant la réplique des octaves : de sorte que l'on fait une bonne Harmonie en répétant l'octave du Lichanos Meson, ou du G ré sol, et celle du Lychanos Hypaton, ou D ré sol, laquelle est composée de ces termes 3, 4, 6, et puis de 6, 8, 12, et finalement de 12, 16, 24, outre lesquels on ne peut passer sans user de répétitions.

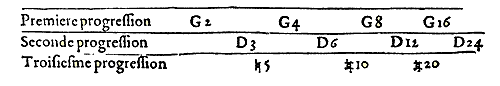
En second lieu, on rencontre six consonances dans l'ocatve divisée en douze demi tons égaux, à savoir la tierce mineure, la majeure et la quarte; et leurs compléments que sont la sixte majeure, la mineure et la quinte.

En troisième lieu, que toute harmonie est engendrée de sons différents et non contigus qui sont tellement commensurables entre eux que l'un peut contenir l'autre et qu'ils sont joints par un lien commun. Parce que les sons se font par des corps, il en faut chercher la raison dans les solides (volumes) et non dans les plans ou dans les lignes. D'où il conclue que l'union des sons fait l'harmonie par l'égalité de l'unisson ou par la ressemblance des autres intervalles.
Ceci posé, il suppose que l'octave est un cube harmonique sur lequel toute l'harmonie est fondée, de sorte qu'elle doit avoir autant d'intervalles harmoniques qu'il y a de cubes semblables, qui peuvent être joints entre eux par le moyen d'un autre, ou de plusieurs cubes moyens parce qu'un cube est semblable à un autre cube et que le cube qui est leur différence leur est aussi semblable, ou qu'il en contient de semblables.
Or la tierce mineure contient trois intervalles, et son complément neuf.
Le cube entier de l'octave qui a 12 intervalles est 17 . 8 (écrit comme ça dans le texte, mais il faut lire 1728).
Le cube de la tierce est 27, celui de son complément 729. La somme des deux est 756. Leur différence d'avec le cube de l'octave est 972, laquelle contient 36 cubes du Diton comme la sixte majeure en contient 64 de la tierce mineure. Partant ces cubes conviennent avec celui de l'octave et se joignent par des cubes semblables.
L'octave entière contient 64 cubes de la tierce mineure et deux cubes de la sixte, plus 10 cubes du Sesquiditon.
La tierce majeure a quatre intervalles et la sixte mineure, laquelle est son complément, en contient 8. Le cube du Diton 64, et celui de la sixte mineure 512, qui font ensemble 576. De sorte que 1152 est la différence d'entre leurs cubes et le cube de l'octave. Cette différence contient 18 cubes du Diton, comme la sixte mineure 8, et l'octave entière 27. Ou 3 cubes de la sixte mineure plus 3 cubes du Diton.

En quatrième lieu, il faut procéder autrement dans la quarte et dans la quinte parce que leur raison n'est pas composée de cubes mais de plinthes ou de parallélépipèdes, car le rectangle solide de la quarte est 720, celui de la quinte 1008, dont la somme fait le cube de l'octave 1728.
Le solide rectangle de la quarte est différent du plinthe de l'octave, c'est à dire de 288, or ils sont huit pour leur commune mesure.
Par conséquent le plinthe de la quarte est égal à 90 cubes et celui de la quinte a 126 cubes. Mais le cube de l'octave est égal à 216 cubes et conséquemment ces deux plinthes sont composés de cubes égaux qui font celui de l'octave. Or ces deux consonances sont les plus parfaites puisqu'elles divisent le cube de l'octave en deux solides rectangles égaux et qu'elles ont le premier cube pour commune mesure.

Quant aux autres consonances, outre les deux cubes, elles considèrent trois solides rectangles qui sont tirés de la division d'un cube en deux cubes semblables. D'où il conclue que l'union, et par conséquent l'harmonie, se conserve quand la division n'est point multipliée et qu'elle se détruit lorsqu'elle s'augmente.

Quant au triton, il contient six intervalles dont le complément est un autre triton. Le cube de l'un et de l'autre est 216 et la somme des deux, à savoir 432, est la différence d'avec le cube de l'octave 1296 qui contient six cubes du triton. L'octave entière contient 8 cubes du triton. Mais cet intervalle n'est pas harmonique, encore qu'il se résolve en cubes égaux et commensurables entre eux, parce qu'il n'y a point de différence entre eux et que l'un ne peut contenir l'autre. D'où il arrive qu'il ne fait point d'union des tons par la réception de l'un et l'autre, mais une collision désagréable. Car l'harmonie veut que l'octave contienne le plus grand intervalle et que le plus grand contienne le moindre afin qu'il y ait une distance commensurable entre les uns et les autres. Il faut néanmoins remarquer que l'harmonie souffre la commensurabilité des cubes du triton par le moyen d'un léger attouchement par lequel on passe à une parfaite harmonie.

La seconde, ou le ton, a deux intervalles dont 8 est le cube. La septième qui est son complément en a 10 et son cube est 1000. La somme de ces cubes font 1008 et la différence d'avec le cube de l'octave est 720 qui contient 90 cubes du ton. La septième contient 125 cubes du ton. L'octave contient tous les cubes de la septième, plus 9. Mais elle ne peut être appelée harmonie, encore que l'octave contienne la septième et la seconde, parce que l'un et l'autre de leurs sons étant contigus aux extrémités de l'octave, ils s'entrechoquent. Bien qu'autrement que dans le triton dont la collision se fait au milieu de l'octave, cette collision est cause que ces sons sont désagréables à l'oreille.