Traité de l'Orgue de
Marin Mersenne.

PROPOSITION XLV. Entre deux lignes droites données , trouver deux moyennes continuellement proportionnelles , pour diviser le Diapason des Orgues en douze demi-tons égaux.

Je veux ici donner un moyen de trouver géométriquement les onze moyennes proportionnelles du Diapason. Ce Diapason dépend d'une seule parabole qui a été trouvé par l'un des plus grands esprits de ce monde dont la modestie est si grande qu'il ne veut pas être nommé. Je n'en eut mis ici que la construction si M. de Roberval ne m'en avait fait promptement la démonstration.
Cette construction est à mon avis la plus simple de toutes celles qui ont été inventées jusqu'à maintenant pour la solution de ce problème, duquel dépend la construction du cube si célèbre et qui a tant été recherché par les Géomètres anciens et modernes.

La solution de ce problème se fait par le moyen d'une seule parabole, du cercle et de la ligne droite.

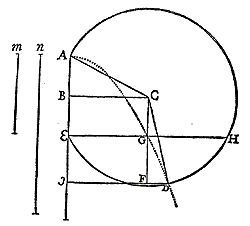Soient deux lignes droites données M , N , desquelles M soit la moindre et qu'entre les deux il faille trouver deux moyennes continuellement proportionnelles.
Soient A E , E H deux lignes droites perpendiculaires l'une à l'autre, desquelles A E soit égale à M et E H égale à N. A E est coupée en deux parties égales au point B duquel est élevée la perpendiculaire B C , de même que E H (au point E) et égale à la moitié de E H.
Soit aussi menée la ligne C A . On trace un cercle ayant pour centre C et pour rayon C A dont la circonférence passera par les points A H E ce qui est facile à démontrer puisque étant prise la ligne A E donnée par position pour l'axe d'une parabole et la longueur de la même A E pour côté droit, soit décrite la parabole A G D coupant la ligne E H au point G et la circonférence du cercle au point D. Il est clair que la parabole coupe la ligne E H perpendiculaire à l'axe A E et qu'elle coupe aussi la circonférence du cercle entre les points E et H. Puisqu'elle s'étend infiniment, le cercle étant fini, elle sortira et coupera la circonférence au point D entre E et H .
Soit donc, du point D sur l'axe A E prolongé, on abaisse la perpendiculaire D I .
D I et A I sont les deux moyennes proportionnelles que l'on demande. Car, soit menée C D et C F perpendiculaire sur I D, laquelle ligne C F tombera ou entre I et D, ou au point D, ou sur I D prolongée au delà du point D.
Qu'elle tombe donc entre I et D, car ce cas étant démontré, les deux autres n'auront aucune difficulté.
Puisque donc D I est coupée en F, il s'ensuit que les deux carrés de D I, I F ou D I, B C sont égaux au carré de D F et à deux fois le rectangle D I F. Mais deux fois le rectangle D I F est égal au rectangle sous D I et N, pour ce que N est double de B C égale à I F. Donc les deux carrés de D I et B C sont égaux au carré de D F et au rectangle sous D I et N.
Semblablement les carrés A I et A B sont égaux au carré B I ou C F et a deux fois le rectangle I A B ou le rectangle seule I A E.
Soient donc ajoutées choses égales à choses égales, à savoir les deux carrés D I et B C aux deux carré A I et A B et le carré D F avec le rectangle sous D I et N au carré C F avec son rectangle I A E.
Alors les quatre carrés D I, B C, A I et A B seront égaux aux deux carrés D F, C F, et aux deux rectangles, l'un desquels est sous D I et N et l'autre est I A E.
Mais des quatre carrés, les deux C B, A B sont égaux au seul A C. D'autre part les deux C F, D F sont égaux au seul C D. A C est égal à C D à cause du cercle.
Soient donc ôtez ces carrés égaux A C, C D et resteront les deux carrés D I et A I d'une part, égaux aux deux rectangles sous D I et N, et sous I A C d'autre part.
Mais le carré D I est égal au rectangle I A E à cause de la parabole de laquelle A E est le côté droit.
Soient donc ôtées ces parties égales et restera le seul carré A I égal au seul rectangle sous D I et N.
Partant la ligne N est à A I comme A I est à I D. Mais A I est à I D comme I D est au côté droit A E ou M, à cause de la parabole.
Donc les lignes N, A I, I D et M sont continuellement proportionnelles.
Les extrêmes M, N sont donnés et nous avons trouvé les moyennes A I et I D qui est ce que l'on demande.

Au second cas, quand la perpendiculaire tombe au point D, les ligne C F et C D sont ensemble et la ligne I D touche le cercle et est égale à B C.
Ce qui arrive quand N, la plus grande des extrêmes données, est octuple en puissance de la moindre des extrêmes M.
Partant, le problème au même cas est plan et les lignes sont continuellement doubles en puissance l'une de l'autre, c'est à dire comme le diamètre d'un carré a son côté, comme il paraît sur la démonstration suivante, laquelle est facile (qu'il dit, le Mersenne ...).
Les carrés A I, A B sont égaux au carré B I, ou C F, ou C D, et à deux fois le rectangle I A B ou au seul rectangle I A E, ou au carré I D, ou B C. Et ajoutant de part et d'autre le carré B C, nous aurons les trois carrés A I, A B et B C aux trois C D, I D et B C. Mais des trois premiers, les deux A B, B C sont égaux au seul A C égal à C D. Soient donc ôtez de part et d'autre les carrés A C, C D et restera le seul carré A I égal aux deux I D, B C. Lesquels, en ce cas étant égaux, le carré A I sera double du carré I D ou du carré de B C. Mais le double du carré de B C, ou I D, est égal au rectangle sous I D et N, pour ce que N est double de B C ou I D. Donc, le carré de A I est égal au rectangle sous I D et N, d'où il s'ensuit que les trois lignes N, A I et I D sont proportionnelles. Le trois A I, I D et A E ou M étant aussi proportionnelles à cause de la parabole. Les quatre N, A I, I D et M seront continuellement proportionnelles, qui est ce que l'on demande.
Et puisqu'il a été prouvé que le carré de A I est double du carré de I D, il parait que les quatre lignes sont continuellement doubles en puissance l'une de l'autre, et que N sera octuple en puissance de M.

Au troisième cas quand la perpendiculaire C F tombe sur I D prolongée au delà de D, ce qui arrive quand la plus grande extrême donnée est plus qu'octuple en puissance de la moindre, la démonstration est entièrement comme au premier cas. Si ce n'est alors que des deux points où la ligne I D coupe la circonférence du cercle, le point D est le plus proche du point I alors qu'au premier cas il est le plus éloigné du même point I.

J'arrête là et vous fait grâce de ses avertissements qui sont tout aussi nébuleux ! Néanmoins, si vous y tenez, écrivez-moi, je vous les enverrai.