Musique et tempéraments
Le tempérament musical
Textes et formules compilés par DGW sur les ouvrages de Pierre-Yves Asselin : " Musique et Tempérament ". Editions Costallat - Paris, 1985
et de Dominique Devie : " Le tempérament Musical ". Société de musicologie du Languedoc - Béziers, 1990.
... et quelques ajouts de mon crû.Enregistrements extraits de la cassette d'accompagnement du livre de Pierre-Yves Asselin. C'est lui qui joue l'orgue de L'université Mac Gill de Montréal après l'avoir accordé dans les différents tempéraments. (Voir "M comme Montréal")
Pour commencer, je reprends à mon compte la phrase de Dominique Devie dans son ouvrage "Le tempérament musical":
" ... la généralisation du tempérament égal est analogue à la multiplication des pylônes électriques, des antennes et des autoroutes : ces innovations ont apporté des facilités mais également ont contribué à gâcher le paysage et à "mécaniser" notre univers. C'est pourquoi je m'oppose à toute justification du tempérament égal, lequel n'a strictement rien apporté sur le plan musical. ... "
Le livre de Dominique DEVIE est réédité; on le trouve là:
http://musicreprints.fr.fm/
MàJ 25 mars 2008
Le système Pythagoricien
C'est le système des anciens, au moins pendant tout le moyen âge.
(Voir
note
qui explique que le système Pythagoricien n'est pas une gamme à
l'origine et comment les Anciens (et les Modernes aussi) l'ont bricolé
pour en obtenir une ).
L'avènement de l'organum qui harmonisait les mélodies en quinte et en
quartes parallèles a adopté le système pythagoricien dont 11 quintes sont
parfaitement pures, c'est-à-dire sans battement.
Pendant tout le moyen âge. on a considéré la tierce comme étant
une dissonance. On faisait donc le maximum de compromis sur la tierce
pour favoriser les quintes les plus pures qui soient.
Une illustration ... pour rire un peu : "La quinte
juste"
(Kaamelott Saison 2 Episode 20)
L'un des textes les plus anciens traitant de ce système serait celui de
Arnaut
de Zwolle ,
en 1450 à Dijon. 11 quintes pures, 1 quinte plus petite d'un comma pythagoricien
généralement placée entre si et fa#.
En effet, si on fait 12 quintes pures de do à si#, entre l'octave du do
et le si# existe un intervalle que l'on nomme le comma pythagoricien.
L'usage de l'époque excluait le mode de si, note avec laquelle il était
impossible de former une quinte en utilisant les notes diatoniques naturelles.
Do - Sol
- Ré -La - Mi - Si - Fa# - Do# - Sol# - Ré# - La# - Mi# - Si# (12
quintes pures)
|-----|-----|-----|-----|-----|-----|-----|-----|-----|-----|-----|-----|
Do (Do) (Do) (Do) (Do) (Do) (Do)
Do (7 octaves pures)
|----------|---------|---------|---------|---------|---------|--------|
|-|
Comma
pythagoricien
Chez Arnaut de Zwolle il s'agit en fait d'une description du rapport de
longueur des tuyaux entre les différentes notes d'un orgue. Ces
rapports étant pythagoriciens (la gamme de Boèce) on en
déduit que l'accord des orgues en est de même.
Notons que, en 1766, Dom Bedos de Celles a la même démarche
pour la construction des tuyaux mais décrit très précisément
le tempérament à tierces majeures pures qu'il faudra appliquer
par la suite. L'absence de la mention de la moindre tierce pure chez Arnaut
nous confirme dans la notion d'accord pythagoricien. Au contraire, il
précise le rapport des tierces majeures comme étant de la
proportion de 81 à 64 (deux tons) et les tierces mineures de 32
à 27 (un ton plus un demi-ton).
Exemple : Upon la-mi-ré - Anonyme XVe siècle.
Mesures 13 à 18 - Les fa# semblent bas. En fait ce sont des solb.
- Les grandes gammes ascendantes sonnent "naturelles". Le système Pythagoricien
favorise le "mélodique" grâce à ses grands tons et ses petits demi-tons
diatoniques .
Ecouter
Le système Pythagoricien
et le tempérament à tierces majeures pures
Des dièses et des bémols :
Lorsque les quintes sont pures, dans le système Pythagoricien, le do#
est plus haut que le réb. La différence est égale à 1 comma Pythagoricien.
Le demi ton chromatique est plus grand que le demi ton diatonique.
Lorsque une ou plusieurs quintes formant une tierce majeure pure sont
tempérées, comme c'est le cas dans le tempérament à tierces pures et le
système Zarlinien, c'est l'inverse. Le do# est plus bas que le réb et
le demi ton chromatique est plus petit que le diatonique.
A l'heure actuelle, ce débat est insignifiant puisque avec le système tempéré égal, les dièses et les bémols sont confondus. Les demi-tons diatoniques et chromatiques sont identiques.
Accord à intonation pure.
L'accord à intonation pure consiste à n'avoir, pour une
oeuvre musicale déterminée, que des quintes et des tierces
majeures sans battement.
Il résulte de la gamme de Zarlino dans laquelle des quintes et
des tierces pures coexistent.
Une telle gamme ne peut se concevoir que par système de muance,
c'est à dire en passant d'un tétracorde à l'autre,
ou, plus vulgairement, en prenant la quinte de l'un pour en faire la tierce
de l'autre.
Un peu comme ceci :
Fa - La - Do - Fa
Do - Mi - Sol - Do
Sol - Si - Ré - Sol
En passant d'un tétracorde à l'autre, on décale les
sons harmoniques du nouvel accord d'un comma syntonique.
(Pas très clair ? voir "Zarlino
et la gamme" ).
Ces systèmes d'accords s'appliquent, en fait, aux claviers expérimentaux
à touches multiples dont le nombre de marches (touches) pouvait excéder
12 par octave. Ce que l'on appelait les " feintes brisées " quand
sur un clavier on pouvait rencontrer à la fois un ré# et un mib, un sol#
et un lab , ou parfois un do# et un réb.
Un système parfait à intonation pure complet nécessiterait un clavier
de 32 marches par octave. (voir la proposition
23
du Traité de Mersenne). Il n'existe aucun témoignage de ce
système appliqué à des claviers à 12 marches par octave mais certaines
oeuvres du répertoire peuvent se prêter à cette expérience, celles qui
ne comportent que peu ou pas de modulations. On parle alors de système
incomplet.
Cette pratique, si elle a existé, impliquait un accord complet de l'instrument
pour chaque morceau interprété, ce qui n'est attesté nul part, sauf dans
le cas où il fallait transformer un mib en ré#, ou sol# en lab, ou encore
un do# en réb. (Encore ce cas était-il plus pratiqué dans le cas d'accords
mésotoniques).
Il est évident que l'orgue est totalement exclu d'une telle pratique
qui n'est réalisable qu'avec un clavecin, un clavicorde ou une
épinette.
Après une courte analyse harmonique de la partition musicale il est possible
de construire soi-même un système incomplet à intonation pure, c'est à
dire comportant à la fois les intervalles de tierces et de quintes purs
propres à l'interprétation du morceau en question.
Exemple : "The Bells", de William Byrd. L 'analyse de " The
Bells " montre que cette oeuvre n'emploie que des accords de do maj, sol
maj et ré min. Plus loin, un sib intervient en tierce majeure du ré. On
peut donc construire un accord avec les quintes do-sol-ré-la pures, les
tierces do-mi, sol-si, ré fa#, la do#, mib-sol, sib-ré, fa-la pures et
aussi mi-sol# (bien que le sol# ne serve pas). Il en résulte d'autres
quintes pythagoriciennes pures : mib-sib-fa et mi-si-fa#-do# décalées
d'un comma syntonique par rapport aux 4 quintes de base.
Dans la partition de " The Bell ", on remarque l'emploi d'un accord de
la mineur qui est inutilisable mais des éléments du contexte de cet accord
interviennent afin de camoufler sa discordance : l 'accord de la mineur
est en premier renversement (do-mi-la), l'intervalle est entendu en quarte
(mi-la), il y a toujours un ornement sur le mi.
Compte tenu des difficultés d'application du système à intonation pure, comme du système de Zarlino, on en est vite arrivé à concevoir un système mitigé, gardant les tierces pures mais en sacrifiant les quintes : l'accord Mésotonique.
Le tempérament au XVIIe siècle
en France
Passage de l'accord Pythagoricien au mésotonique.
La musique de clavier peut fournir un témoignage en faveur de l'un ou l'autre tempérament.
Le Buxheimer Orgelbuch qui date de 1470 montre des tenues sur ré-fa#, la-do# et mi-sol#. Or ce sont de " bonnes " tierces pour un accord Pythagoricien avec fausse quinte entre si et fa# (quinte diminuée du comma pythagoricien).
Tout converge pour indiquer que l'entrée dans les moeurs du tempérament
à tierces pures s'est faite à partir de 1450. La première description
n'a néanmoins eu lieu qu'en 1523, Aron étant le premier auteur
à décrire le tempérament où chaque quinte est diminuée d'un quart de comma
syntonique.
Elle a de toute façon été faite sans ambiguïté par Zarlino
en 1571, celui-ci précisant qu'il était en usage bien avant lui.. Reste
à savoir comment s'est faite la transition du Pythagoricien au mésotonique.
Or l'essentiel de la pratique se transmettait oralement et les musiques
écrites étaient avant tout des canevas, toute harmonisation ayant pu être
faite dans le système utilisé à son l'époque. Tout ce que l'on peut admettre,
c'est que les praticiens élargissaient légèrement leurs tierces pures.
Pour ce qui est de la musique populaire, il est fort probable que l'accord
Pythagoricien a pu durer plus longtemps.
Tempéraments mésotoniques
A l'arrivée de la renaissance et de ses grandes polyphonies, on a voulu
reconnaître la tierce majeure comme consonance et, à l'inverse du système
pythagoricien, le tempérament mésotonique (ton moyen) fait le maximum
de compromis sur la quinte afin de se procurer le maximum de tierces pures,
par diminution des quintes de un quart de comma syntonique.
Ce tempérament est classé parmi les systèmes réguliers car toutes les
quintes ont la même valeur sauf une, la quinte du loup (Dominique
Devie voit dans ce terme de loup une origine cosmologique. Pour ma part,
je pense qu'il s'agit plus prosaïquement de la quinte loupée !).
En anglais, c'est le Meantone, le medio-tono des italiens et le Mitteltönig
des allemands.
L'expression " ton moyen " est considérée par rapport à la tierce plutôt
qu'en rapport au ton car cette dernière y est partagée en deux parties
parfaitement de même valeur (ils s'agit de deux tons moyens, ni majeurs
ni mineurs).
Le mésotonique classique à tierces majeures pures comporte un maximum
de 8 tierces majeures pures :
mib>sol, sib>ré, fa>la, do>mi, sol>si, ré>fa#, la>do#,
mi>sol#.
Les quatre autres tierces sont difficilement supportables. Elles sont
trop grandes d'un comma enharmonique par rapport aux tierces majeures.
Elles sont en fait 4 quartes diminuées.
La quinte du loup est généralement pratiquée entre sol# et mib qui est
trop grande de 1 3/4 de comma syntonique. C'est presque une sixte.
Ce
tempérament ne permet que les tonalités comprises entre sib majeur et
la majeur. La différence entre degrés chromatiques et degrés diatoniques
est très accentuée.
Le sol# ne peux pas servir de lab, pas plus que le mib et le sib ne peuvent
servir de ré# et de la#.
Sur un clavecin, ces notes peuvent être réaccordées rapidement en fonction
de la pièce à jouer mais sur l'orgue c'est ce qui avait conduit certains
facteurs d'instruments, particulièrement en Italie et en Espagne, à poser
deux touches entre le ré et le mi, et entre le sol et le la (feintes brisées).
Un seul cas connu en France, datant de Crépin Carlier en 1632, l'orgue
de Saint
Nicolas des Champs,
qui en a vu la suppression des mains même de Louis Alexandre Clicquot,
le père de François-Henri, en 1732.
9 tierces mineures sont réduites d'un quart de comma, comme les quintes.
Elles donnent des battements mais produisent une impression de grande
justesse.
Les trois autres, très étroites, sont presque des secondes augmentées
: mib>fa#, sib>do# et fa>sol#.
Exemple :
Cantique à l'Immaculée conception, F.C. de Arauxo, mesures 1 à 8
Grande pureté due aux tierces majeures pures.
Ecouter
Mesures 57 à 64 et 113 à 119. Mesure 59, le si est bas. Les demi-tons
diatoniques sont grands, contrairement au Pythagoricien. La tierce mineure
sol>sib sonne " petit ".
Ecouter
C'est la caractéristique des tierces mineures de ce tempérament. Les petits tons et les grands demi-ton se font sentir, à l'opposé du Pythagoricien. Le mésotonique est un tempérament qui favorise davantage l'harmonie que la mélodie.
Justification de l'accord à
tierces pures.
Un texte de Henri Legros dans "Connaissance de l'Orgue",
N° 28 & 29.
Ce texte est très intéressant pour la compréhension
de l'accord mésotonique.
Pour décrire un accord, il est d'usage de disposer en cercle le cycle des quintes.
On y voit que l'octave est composée de 12 quintes qui, un peu
comme dans un lit de Procuste, ne peuvent pas toutes y être en leur
pleine valeur pure. On le sait depuis Ptolémée.
On y voit surtout qu'une tierce majeure est composée par quatre quintes
successives. En fonction de la valeur des quintes qui les composent, elles
sont plus ou moins grandes.
Do .................
Fa ! Sol . ! . Sib ! Ré . ! Tierce majeure Mib -------- ! -------- La . ! . Sol# ! Mi ....... ! Do# ! Si Fa#
Le comma syntonique est la différence, pour Do à Mi par exemple, entre un Mi issu des quatre quintes pures successives Do-Sol-Ré-La-Mi et un Mi pur par rapport à Do (tierce pure).
Do
- Sol -
Ré - La
- Mi
(4 quintes pures)
|-------------|-------------|-------------|-------------|
Do (Mi) (Do) (Mi) (Do) Mi
(Accord pur avec Do)
|------|---------------|------|----------------|------|
|-|
Comma
syntonique
Le rapport de ce comma syntonique est de 81/80. Il vaut 21,5 cents et
5,395 savarts.
Si on retire un quart de comma syntonique à 4 quintes successives, la
tierce qu'elles composent se trouvera pure.
Par contre, ce 1/4 de comma syntonique est nettement plus grand que le
1/12 de comma pythagoricien que l'on retire dans l'accord tempéré
égal moderne. Le rattrapage (le "loup") se fera sur la
douzième, la moins usitée, placée entre Sol# et Mib,
qui sera alors beaucoup trop grande. Presque une sixte.
On appelle “pur” un accord ne produisant pas de battement.
Do------------------------
Fa -1/4 ! -1/4 Sol | -1/4 ! -1/4 de comma syntonique Sib ! Ré | -1/4 ! -1/4 |La tierce Pythagoricienne Mib -------- ! -------- La |diminuée de 1 comma loup (+7/4)! -1/4 |syntonique devient pure. Sol# ! Mi-------------- -1/4 ! -1/4 Do# -1/4 ! -1/4 Si Fa# Mésotonique à 8 tierces pures
Exemples musicaux :
Cantique à l'Immaculée conception, F.C. de Arauxo.
Toccata settima - Rossi
Note : Couleur accordale d'un accord mésotonique avec tierce
majeure pure :
Lorsqu'un accord de 3 sons est joué à l'état fondamental, par exemple
do-mi-sol avec tierce majeure do>mi pure, le rythme de battement de
la quinte est perçu deux fois moins rapidement que quand celle-ci est
jouée seule. Cette impression est donnée par l'interaction des sons résultants
provenant des 3 notes impliquées.
(On appelle "son résultant" un son fondamental que l'on
entend quand on ne joue que deux ou trois de ses harmoniques alors que
ce son fondamental lui même n'est pas émis. Ils sont particulièrement
audibles quand deux flûtistes jouent ensemble; on perçoit
nettement une troisième note, plus grave, qui est la fondamentale
de l'accord des deux notes émises par les flûtes).
Ecouter un son résultant : Les 3 notes, jouées séparément,
font entendre un son plus grave quand elles sont jouées ensemble.
Voir la page sur les sons résultants : sons
différentiels et complémentaires
Une méthode d'accord au tempérament mésotonique
Pour le mésotonique à 8 tierces pures, on accorde, à partir d'un Do de référence, la tierce Do>Mi.
Le "La" comme diapason est très récent. Il ne correspond à rien sur
un clavier et - historiquement - à aucun tétracorde. "Avant", on commençait
par un Do ou un Fa.
La première note que je cite est la note de référence, la seconde, celle
qu'on accorde).
Donc, à partir du Do de référence, on accorde la tierce Do>Mi pure.
Ensuite, on équilibre les quatre quintes entre Do et Mi: Do>Sol, Sol>Ré,
Ré>La et La>Mi en ajustant le Sol, le Ré et le La de manière à ce
que ces 4 quintes (ou quartes en descendant) aient un nombre de battements
à peu près identiques. Les quintes doivent être un peu trop petites
du 1/4 de comma, donc les quartes un peu trop grandes.
On doit obtenir à peu près 4 à 5 battements par seconde pour ces quintes
dans la troisième octave d’un jeu de 4 pieds (prestant).
Donc on accorde le Sol sur le Do, pur dans un premier temps (voir
nota*), puis on le descend, jusqu'à obtenir 4 à 4,5
battements par seconde, sur la 3e octave d'un jeu de 4 pieds.
Puis, en descendant, on accorde le Ré sur le Sol, quarte descendante un
peu trop grande, donc le Ré plus bas que pur. Cette quarte en descendant
doit battre plus vite que la quinte, d'une valeur de 3 pour 2, c'est à
dire 6 à 7 battements par seconde.
Puis on accorde le La sur le Ré un peu plus bas que pur. (C'est
simple, la note à accorder doit toujours être plus basse).
Même nombre de battements que Do>-Sol.
Puis on vérifie si la quarte en descendant La> Mi a un nombre de battements
à peu près identique à la quarte Ré>Sol et qu'elle est
bien un peu grande. Pour vérifier, on descend le La qui doit devenir
pur. Si c'est le cas, on le remet à sa place, sinon c'est qu'on
s'est planté quelque part et on recommence !
(Pour "descendre" le La sur un Prestant, il suffit
d'approcher un objet - l'accordoir - ou la main au sommet du tuyau :
les battements doivent ralentir. Ca évite de le désaccorder).
A partir de cette "quadrature", on finit l'accord avec les autres tierces
pures (en descendant ou en montant suivant le cas) Sol<Mib, Sol>Si,
La<Fa, La>Do#, Ré<Sib, Ré>Fa#. Enfin, Mi>Sol#.
Sauf erreur, on a toutes les notes.
On vérifie la qualité des quintes, des fois que ... Et voilà. Toutes les
quintes sont réduites de 1/4 de comma syntonique, sauf le "loup" Sol#>Mib
qu'on n'a pas accordé et qui, lui, est trop grand de 7/4 de comma
syntonique (+ le schisma).
Pour terminer, on accorde les octaves, pures, en vérifiant que la quarte
inférieure ait le même nombre de battements que la quinte supérieure.
Par exemple, la quarte Do>Fa doit battre comme la quinte Fa>Do supérieure.
Quoique, si on "tire" un peu l'octave, l'accord sera plus coloré,
mais il ne faut pas de battement.
On peut illustrer cette façon : (on accorde les notes rouges
sur les bleues)
On partira d'un Do3 sur un jeu de prestant (4 pieds). Sur un clavecin
aussi mais il faut alors savoir que les battements d'un jeu de 8 pieds
seront deux fois plus lents. 2 à 2,5 par seconde pour les quintes
réduites du quart de comma. 3 à 4 pour les quartes.
Ré4- Mi4- Si3= Do#4= puis Ré4
Mi3= Sol3- \ La3- \ puis Sol3 puis
La3 \
Sib3= Fa#3=
Sol#3=
Do3 puis Do3 Ré3= Mi3= Mib3= Fa3= Do#3= puis Ré3 enfin, Mi3
(preuve)
Ou encore, en restant dans l'octave 3 (enfin, presque) :
Mi3= Sol3- La3- Si3= Do#4= Fa#=3 Sib3= Sol#3=
Do3 puis
Do3 \ / Mi3 puis
Sol3 puis
La3 \ puis
Ré3 /
enfin, Mi3
Ré3- (Preuve) Fa3=
Do#3= Sib2=
"-" veut dire que la note est un peu basse, et "=" que la note donne un accord pur.
Tout le reste du clavier se fera par octave en vérifiant quartes et quintes.
Si on part d'un La, on équilibre les 4 quintes Do - Sol - Ré
- La - Mi à partir du La jusqu'à ce qu'on obtienne Do -
Mi pur sans retoucher au La.
Ou alors on part d'un Do haussé de 10 cents.
(Nota*) Cette pratique ne vaut que pour des tuyaux entaillés, pavillonnés ou bagués, pour les tuyaux à anche ainsi que pour le clavecin. Il est évident que si on accorde des tuyaux "coupés au ton", il est difficile de monter le ton d'un tuyau puis de le redescendre. On l'éreinte. Dans ce cas, on ne peut pratiquer que par approche, tel que le décrit Dom Bedos de Celles.
Evolution du tempérament inégal en France au 18e et au début du 19e siècle.
Les sources sont assez nombreuses, une douzaine environ, de 1726 à 1797.
Il s'agit d'un mésotonique modifié dont l'évolution s'est amorcée dès
le milieu du 17e siècle.
On assiste au fil du temps à une "irrégularisation harmonieuse"
de la formule régulière de départ. Du point de vue structurel, l'octave
tend à être divisée en trois tierces de largeur progressive, division
qui ressort assez clairement chez d'Alembert.
On peut imaginer une infinité de formule jusqu'à ne plus avoir de tierce
pure, l'altération des quintes étant progressive pour ne plus avoir de
quinte outrée (loup) en fin de cycle.
Le répertoire de la musique d'orgue montre que l'accord de cet instrument a peu varié au cours du 18e siècle. Il est demeuré avec un grand nombre de tierces pures et la musique ne modulait pratiquement pas. On trouve quelques Lab et quelques Ré# mais aucune modulation au delà de ces tonalités qui épousaient les tons communs de l'Eglise. Ces quelques notes étrangères tendraient à prouver que, faute de feintes brisées, certains orgues pouvaient bénéficier d'un accord "adouci". Nous y reviendrons.
C'est au clavecin que les compositeurs se sont beaucoup plus
hasardés à faire des modulations, ce qui a provoqué (ou ce qui a été motivé
par…) l'apparition de tempéraments possédant de moins en moins de tierces
pures et une quinte du loup de moins en moins flagrante.
Chaumont en illustre un premier stade, qui s'est poursuivi avec
Rameau, Marpurg, puis d'Alembert, Rousseau
et Bethisy (ces deux derniers ont en fait compilé froidement d'Alembert,
y compris une erreur que nous verrons plus tard !). Chez ces derniers,
il ne reste plus qu'une seule tierce pure.
Le répertoire pour clavecin du 18e siècle exige donc des tempéraments assez évolués et les solutions des textes anciens présentent une grande variété de qualités expressives d'intervalles.
Et malgré tout ça, Dom Bedos de Celles a décrit dans " L'art
du facteur d'orgue ", en 1766, un tempérament parfaitement mésotonique
à 8 tierces pures (ou presque*), ce qui prouve, sinon le retard, au moins
la forte tradition de la facture d'orgue au 18e siècle. Ce tempérament
a perduré jusqu'à, pratiquement, la fin du 19e siècle, au fil des restaurations
et de la modernisation des orgues classiques par les Merklin ou autre
Cavaillé-Coll.
Ce n'est qu'en 1871 que Merklin accorda l'orgue de la cathédrale de Poitiers
en "égal".
* En fait, Dom Bedos de Celles adoucit quelque peu (très
peu) ce tempérament qu'il qualifie "d'ancienne partition",
en bricolant un peu le cycle des quatre quintes qui servent à obtenir
la tierce Do - Mi pure, et en raccourcissant la huitième tierce,
Si bémol - Ré. Voir plus loin.
Lambert-Chaumont.
Mort en 1712 à Huy, en Belgique, ce curé organiste nous a laissé un seul recueil de pièces d'orgue dans les 8 tons qui se trouve au conservatoire royal de Liège. Sa méthode d'accord est destinée au clavecin, l'orgue conservant généralement un mésotonique à 8 tierces pures.
La partition de Lambert-Chaumont propose deux possibilités : les quintes
Sib>Fa et Mib>Sib sont dites fortes ou faibles.
Sol#>Mib apparaît toujours comme le défaut de l'accord. Si les quintes
sur Mib et Sib sont faibles, nous avons le tempérament à tons moyens standard.
"On peut cependant tenir ces deux bémols forts, mais en ce cas il faut
ménager les autres quintes à l'advenant et il est sûr que si l'on observe
la méthode susdite qu'on la trouvera plus facile et plus agréable"
.
La tierce mineure d'Ut est acceptable, par contre, celle de Fa est grinçante.
Notons qu'à l'époque, Nicolas de Grigny utilisait le Ré# et le Lab. L'orgue
de la cathédrale de Reims avait-il des feintes brisées ou un tempérament
évolué ? (Probablement des feintes brisées, vu sa
date de construction!)
Caractéristiques du tempérament de Lambert-Chaumont : 6 tierces majeures
pures, de Fa>La à Mi>Sol#. Un loup moins "défectueux" en fonction
de la qualité donnée aux quintes Sib>Fa et Mib>Sib.
Chaumont suggère de les conserver plus petites que pure si on veut un
tempérament mésotonique authentique, ou bien plus grandes que pures si
on désire obtenir une tierce supplémentaire en rendant Si>Ré# plus
consonant.
Les tierces Sib>Ré et Mib>Sol se mettent à battre, Mib>Sol étant
plus grand que Sib>Ré.
Tempérament de Chaumont
Do
Fa -1/4 ! -1/4 Sol 0+ ! -1/4 Sib ! Ré 0+ ! -1/4 Mib -------- ! -------- La loup ! -1/4 Sol# ! Mi -1/4 ! -1/4 Do# -1/4 ! -1/4 Si Fa#
Dans le mésotonique classique, on a -1/4 de comma entre Mib et Sib et entre Sib et Fa. Chez Chaumont, la tierce Sib>Ré qui "contient" une quinte pure ou un peu grande battra moins que la tierce Mib>Sol qui en "renferme" 2. Le Mib pourra servir de Ré#
Exemple : Plein-jeu de la deuxième suite de Louis-Nicolas
Clérambault
Mesure 31 à 36, effet dramatique du Lab qui est en fait un Sol#, du à
la grande distance le séparant du Sib et du Do (mesure 33). La tierce
Lab>Do, très dure, est adoucie par la tenue sur le Sib.
Ecouter
Mesure 41 à 46, intervalle Fa#>Sib dissonant donnant le caractère
d'une grande douleur à ce passage.
Ecouter
Le tempérament de Corrette
Donné en 1753, un tempérament décrit par Corrette est très semblable à celui que le sieur Vincent a énoncé en 1712. Facteur d'orgues à Rouen, Boyvin considérait Vincent comme "un très habile homme de son métier" et lui confia l'orgue de la cathédrale de Rouen.
CORRETTE fait réduire d'un quart de comma 8 quintes au lieu de 11, ce
qui donne les 5 tierces justes Fa>La, Do>Mi, Sol>Si, Ré>Fa#
et La>Do#.
Ce tempérament est très proche de celui de Lambert-Chaumont. Il comporte
seulement une quinte forte supplémentaire et une tierce pure de moins
(au nombre de 5). Dès lors, le Sol# peut servir de Lab.
Do
Fa -1/4 ! -1/4 Sol 0+ ! -1/4 Sib ! Ré 0+ ! -1/4 Mib(Ré#) --- ! -------- La loup ! -1/4 Sol#(Lab) ! Mi 0+ ! -1/4 Do# -1/4 ! -1/4 Si Fa# Corrette (Vincent)
Corrette a aussi décrit la partition anglaise de Keller (1707) qui semble n'être qu'une description du tempérament régulier classique au quart ou au cinquième de comma syntonique. Il décrit aussi une partition qui n'est autre que le tempérament égal qu'il baptise "nouvelle partition". Beaucoup d'auteurs ont décrit cette "nouvelle partition" tout en ne cachant pas leurs réticences et l'on sent une concession sans profondeur à une mode dont il n'ont rien à faire.
Rameau
Dans le "Nouveau système de musique" Rameau décrit, en 1726, une partition qui était courante à son époque et qui est désignée comme étant "le tempérament ordinaire". Ce tempérament dont on parlera jusqu'en 1780 s'oppose à "la nouvelle partition" qui est le tempérament égal, lequel ne sera réellement adopté qu'au terme de la première moitié du 19e siècle.
Les passages essentiels du texte
de Rameau.
La description de Rameau est l'archétype de la version "moyenne" d'un
mésotonique modifié que de nombreux auteurs décriront en se recopiant
les uns sur les autres.
L'intérêt de la description de Rameau est qu'il donne deux versions du
même tempérament, l'un commençant par l'Ut, favorisant les dièses, l'autre
commençant par le Sib, favorisant les bémols.
Le tempérament qu'il décrit comporte 7 quintes réduites de ¼ de comma
syntonique en rendant les cinq autre quintes "un peu plus justes" à partir
du Do# dans le premier cas, et du Si dans le deuxième.
(Si#)Do
(Mi#)Fa 0- ! -1/4 Sol 0+ ! -1/4 (Sib)La# ! Ré 0+ ! -1/4 (Mib)Ré# ------- ! -------- La 0++ ! -1/4 Sol# ! Mi 0- ! -1/4 Do# -1/4 ! -1/4 Si Fa# Rameau (en do)
Do
Fa -1/4 ! -1/4 Sol -1/4 ! -1/4 (La#)Sib ! Ré 0- ! -1/4 (Ré#)Mib ------- ! -------- La 0 ! -1/4 (Sol#)Lab ! Mi 0+ ! -1/4 (Do#)Réb 0++ ! 0- Si Fa# Rameau (en sib).
C'est le même, mais décalé de deux quintes ! Il n'y a plus de quinte du loup (si ce n'est une quinte un peu plus grande que pure), 4 tierces majeures pures, les autres tierces étant progressivement altérées au rythme de la disparition des quintes diminuées de 1/4 de comma syntonique dans leur constitution.
Exemple musical : L'enharmonique, de Rameau
Gallimard
Gallimard, (Théorie des sons, 1754), apporte des précisions quant aux tempéraments de Rameau et en propose un troisième, compromis des deux premiers.
Marpurg
On retrouve aussi ce compromis chez Marpurg (ou Marpourg) dans son "Principe
de Clavecin" de 1756. Pour vendre son manuel, il a dû sacrifier aux goûts
d'un public "attardé" (sic : Devie).
Il propose "la meilleure des partitions qui soient en usage" après
avoir mis en avant un tempérament égal obtenu en divisant l'octave en
trois tierces de même dimension, en référence à Sorge.
Sa formule inégale est le compromis entre les deux tempéraments de Rameau,
en faisant commencer la sienne sur le Fa :
7 quintes "foibles" de Fa à Fa# donnant 4 tierces majeures pures,
5 quintes "moins foibles". En fait, elles sont légèrement plus
grandes que pures.
Do
Fa -1/4 ! -1/4 Sol 0+ ! -1/4 (Sib)La# ! Ré 0+ ! -1/4 (Mib)Ré# ------- ! -------- La 0+ ! -1/4 (Lab)Sol# ! Mi 0+ ! -1/4 (Réb)Do# 0+ ! -1/4 Si Fa# Marpurg
D'Alembert - Elémens de Musique - 1752
Jean Le Rond D'Alembert
Sa description apporte des éléments intéressants dans la mesure où il expose une tripartition de l'octave en 3 tierces.
Par comparaison, la description de Rameau est assez laborieuse, laissant
une imprécision quant à la valeur des quintes non réduites.
On a à faire à 4 groupes de quintes : Do à Mi, réduites de ¼ de comma
syntonique afin d'obtenir la tierce Do>Mi pure, Mi à Sol# à peine plus
petites que pures, et, en descendant, Do à Sol# à peine plus grandes que
pures, le but étant d'avoir le même Sol# à la sortie ! Il ne reste plus
qu'une seule tierce majeure pure.
Dans l'édition de 1752 une erreur est à signaler : après avoir demandé
d'accorder les quintes ascendantes jusqu'à Sol#, il demande d'accorder
les quintes descendantes de Do jusqu'à Réb (au lieu de Mib), ce qui obligerait
à réaccorder le Sol# déjà accordé.
Les éditions postérieures corrigent cette erreur en arrêtant les quintes
descendantes au Lab qui doit correspondre avec le Sol# déjà accordé. Cette
erreur serait sans importance si elle ne se retrouvait pas chez Rousseau
et chez Bethisy !
Do
Fa 0+ ! -1/4 Sol 0+ ! -1/4 (La#)Sib ! Ré 0+ ! -1/4 (Ré#)Mib ------- ! -------- La 0+ ! -1/4 Sol#-Lab ! Mi 0- ! 0- (Réb)Do# 0- ! 0- Si Fa# D'Alembert
Exemple musical : Benedictus de la messe pour les Paroisses
de François Couperin.
Mesures 19 à 24 : Les intervalles sont moins contrastés qu'en mésotonique.
On remarque cependant le contraste d'une petite tierce mineure ré>fa,
un grand ton fa>mib, un petit demi-ton mib>ré. L'impression produite
est toujours due à une alternance entre ces grands et ces petits intervalles.
Mesure 19 à 21, la quinte tenue sol>ré produit un battement de quinte
mésotonique. Ce battement disparaît après la résolution du ré sur le do.
Mesures 22 et 23, opposition de deux trilles sur un petit demi-ton mib-ré
et un grand demi-ton sur ré-do#
. Ecouter
Rousseau - Dictionnaire de la musique - 1767
On retrouve l'erreur de l'édition originale de d'Alembert.
Rousseau a une tenace réputation de plagiaire et on y retrouve
d'ailleurs des phrases entières du dictionnaire de Sébastien de Brossard
paru 60 ans plus tôt.
(Réputation tenace qu'un visiteur réfute.
Voir son courriel )
Cependant, dans sa "Dissertation sur la musique moderne" parue
en 1763, Rousseau décrit les couleurs attachées aux tonalités usuelles,
preuve que le tempérament au 1/12e de comma était "loin d'avoir imposé
sa tyrannie" (sic : Dominique Devie).
Parlant du tempérament égal, Rousseau écrit : "Malgré l'air scientifique
de cette formule, il ne paroît pas que la pratique qui en résulte ait
été jusqu'ici goûtée des musiciens et des facteurs : les premiers ne peuvent
se résoudre à se priver de l'énergique variété qu'ils trouvent dans les
diverses affections des sons qu'occasionne le tempérament…"
Un site très complet sur Rousseau, publié par le professeur
Yoshihiro Naito:
http://www.osk.3web.ne.jp/~nityshr/index.htm
Un autre site recommandé par "Alexandre", un visiteur,
dont on peut voir le courriel
qu'il
m'a envoyé en m'apportant des précisions très intéressantes:
http://rousseaustudies.free.fr/
Manuscrit anonyme de Caen
L'accord décrit dans un document dit "Anonyme de Caen" a été rédigé en 1746 par un certain PBC dans le cadre d'un traité plus complet et qui concerne plus particulièrement l'orgue Lefèvre de Saint Etienne de Caen (1741).
LA MANIER DACORDE POUR FAIRE LA PARTION JUSTE
"Il faut premierment maitre lute du milieu du clavier en ton ensuitte maitre son octave d'en bas juste ensuite sa quinte en montant qui est le sol cette quinte soit batante ensuite la quinte du sol en montant qui est le ré cette quinte doit être batante ensuitte son octave dans bas qui soit juste prendre la quinte qui est le la, cette quinte batante prendre sa quinte qui est le my cette quinte batante ensuitte son octave qui soit juste ensuitte sa quinte qui est le sy qui doit être batante la quinte du sy est le fa dièze en montant qui doit être batante ensuitte son octave dans bas qui soit juste prendre sa quinte en montand qui est l'ute dièze qu'elle soit battante ensuitte son octave dans bas ensuitte sa quinte qui est le la dièze (sic) qui doit être un peu forcé on reste là toute ces quinte doive battre egalle et les octave bien juste il faut reprendre votre ut du milieu avec sa quinte dans bas qui est le fat naturel cette quinte soit batante ensuite son octave dans haux prendre sa quinte en decendans qui est le sy bemol cette quinte doit être juste ensuite sa quinte en descendans qui est le my bemol cette quinte doit être forcé ensuite son octave dan haut juste le reste par octave"
D'une parfaite imprécision, cette manière d'accorder
est actuellement le refuge de ceux qui veulent revenir à un accord
ancien sur un orgue ou l'on ne retrouve plus grand chose d'authentique
en matière de tempérament. "- Tiens, on a retrouvé
le tempérament de l'Anonyme de Caen ... "
(Pour moi aussi, c'est pratique: quand je foire un "Rameau"
sur mon positif, je prétend avoir fait "l'Anonyme de Caen").
La seule chose tangible est la répartition du "loup" sur les trois quintes Do#>Sol# (d'ailleurs l'Anonyme parle par erreur du La# au lieu du Sol#), Sol#>Mib et Mib>Sib et sur la quinte Sib>Fa qui est pure.
l'Anonyme
de Caen ?
Dom Dedos de Celles
Célèbre pour avoir rédigé un ouvrage très
complet et très détaillé sur la facture d'orgue,
"L'Art du Facteur d'Orgues", en 1770, ce Bénédictin
que d'aucun qualifie de "maniaque de l'ustensile" décrit
un tempérament très proche du Mésotonique d'origine,
à quelques petits détails près.
Il commence par nous indiquer "On trouvera
qu'il y a 8 quintes de 34 comma, qui sont par conséquent égales
entre elles. Ce sont : Ut>Sol ; Ré>La ; La>Mi ;
Mi>Si ; Fa dièze>Ut dièze ; Ut dièze>Sol
dièze ; Mi bémol>Si bémol ; Fa>Ut.
Il y en a trois de 33 comma, qui doivent être un peu plus affaiblies
que les huit précédentes ; ce sont : Sol>Ré ;
Si>Fa dièze ; Si bémol>Fa.
Il en reste une dont l'intervalle est plus grand qu'il ne faut, qui est
de 35 comma ; c'est Sol dièze>Mi bémol.
Les ouvriers appellent cette quinte, la quinte du loup.
Les tierces majeures sont au nombre de 12. On trouvera qu'il y en a 7
de 19 comma ; celles-ci sont parfaitement justes, qui sont : Ut>Mi ;
Sol>Si ; Ré>Fa dièze ; La>Ut dièze ;
Mi>Sol dièze ; Mi bémol>Sol ; Fa>La.
Il y en a une de 18 comma ; celle-ci est un peu faible, mais cependant
encore harmonieuse; c'est Si bémol>Ré.
Il y en a trois de 20 comma, qui sont : Si>Mi bémol ; Ut
dièze>Fa ; Sol dièze>Ut ; celles-ci sont
outrées.
Il en reste une qui l'est encore davantage, c'est Fa dièze>Si
bémol, qui est de 21 comma.
Il faut remarquer que de 12 quintes dont l'octave est composée,
on n'en accorde que onze : la douzième, qui est la quinte
du loup, se trouve d'elle-même au point où elle doit être".
Des 4 quintes qui constituent la tierce pure Do>Mi, à
savoir Do>Sol>Ré>La>Mi, il affaiblit plus la
quinte Sol>Ré que les trois autres. "Si
la tierce se trouve bien juste sans battement, que les trois quintes soient
également tempérées, et la quinte Sol Ré soit
tant soit peu plus affaiblie que les trois autres, on sera
assuré que le plus difficile de la partition est bien fait".
L'explication en est qu'il accorde le Ré4 sur le
Sol3, dans la partie supérieure de la 3e octave. Effectivement,
cette quinte doit battre plus vite, en fait autant que la quarte en descendant
Sol3<Ré3 qui devra être à peine un chouïa*
plus rapide que la quarte Do3>Fa3.
* (Le "chouïa" est à peu près égal
à la valeur de l'épaisseur d'un poil de grenouille).
Ensuite il continue le cycle des quintes afin d'obtenir des tierces pures,
jusqu'au Sol # en montant. Puis en redescendant, il fera la quinte
Do<Fa pour obtenir une tierce Fa>La pure, mais affaiblira
Fa<Si bémol afin que la tierce Si bémol>Ré
batte lentement : "On fera la preuve on comparant ce Si bémol
avec le Ré le plus voisin ; cette tierce
doit être un peu faible et battre lentement"
On peut voir là le texte complet de Dom Bedos : Manière
d'accorder l'orgue.
Et après ?
Mercadier
Mercadier introduit en 1776 la notion " d'élargissement " progressif des quintes autres que les 4 quintes correspondant à la tierce Do-Mi qui reste pure. Il décrit aussi un tempérament au 1/6 de comma, qui se rapproche de l'accord de l'allemand Neidhart, ce qui suggère une possible influence germanisante, ou alors il a pu s'inspirer de Romieu ? de Silbermann ?
Voir "autour du tempérament
de Mercadier",
un texte de Henri Legros.
Loüet
En 1797 Loüet se rapporte à un tempérament dérivé de Rameau et,
ce qui est intéressant, l'applique au piano-forte.
Il est aussi question, dans l'une de ses procédures, d'une quinte ré>la
très faible, ce qui fait penser au premier tempérament de Kirnberger.
"La tradition commence à se perdre et les sources se mélangent" soulève Dominique Devie.
A l'aube du 19e siècle, Armand François Nicolas Blanchet propose en 1801 une méthode à l'interprétation difficile mais qui n'est pas l'égal.
Haüy
Dans son traité de physique en 1806, Haüy déclare que le tempérament égal décrit par Rameau donne des tierces dures et choquantes…
Méthode pour accorder le pianoforte - 1815-1830 :
Cet opuscule présente l'accord égal ainsi qu'une partition inégale correspondant au tempérament de d'Alembert.
J.B. Biot
Dans son traité de Physique, en 1816, Biot se fait l'écho de la préférence des musiciens pour "le tempérament ordinaire".
De Momigny
En 1818, de Momigny reproduit, dans son Encyclopédie méthodique, l'article "tempérament" de l'encyclopédie de Rousseau. Mais, en 1823, il s'est converti à l'égalité.
De Prony
En 1832, le Baron de Prony, l'inventeur du système métrique musical (chiffrage en "cents"), donne l'interprétation de l'ancien tempérament en usage. La formule qu'il décrit est un tempérament régulier au quart de comma où les 4 quintes descendantes sont fortes de +5/22e de comma syntonique.
Montal
L'ouvrage de Montal en 1836 passe en revue certains systèmes antérieurs encore en usage, y compris des auteurs fantaisistes et fait la promotion du tempérament égal.
Pleyel
dès 1797, Pleyel décrit le tempérament de Kirnberger parcequ'il est simple à réaliser mais le fait commencer par le réb et non par l'ut. (On verra ça plus loin !). La seconde partition de Pleyel "pour le concert avec les vents" (dont la gamme est en principe naturelle) comporte des quintes "fortes" et "faibles" et se termine par une quinte sol#>mib dont la justesse sert de preuve.
Cavaillé-Coll
Le
plus célèbre des facteurs d'orgues du XIXe siècle,
avant de répandre le tempérament égal, appliquait
un tempérament subtilement inégal.
A Saint-Denis,
lors de la dernière restauration (1987) de cet orgue construit
en 1841, on trouva : "En remettant les oreilles bien droites
et perpendiculaires aux bouches, on a constaté, dès le début de la mise
en harmonie de l'orgue, dans la deuxième octave de la Montre de 8 pieds
notamment, un tempérament inégal très doux caractérisé par une tierce
Do>Mi pure et les trois tierces Ré>Fa#, Fa>La et Sol>Si presques
pures. Ce tempérament est le seul qui ait permis de conserver à tous les
tuyaux anciens jamais recoupés leur longueur d'origine".
Quelques années avant, un relevé avait été
réalisé sur un "Poïkilorgue*", instrument
à anches libres ne se désaccordant pas, par définition.
On** y a découvert :
7 "bonnes" petites tierces Do>Mi, Ré>Fa#, Fa>La,
Mib>Sol, Sol>Si, La>Do#, Sib>Ré.
1 tierce du tempérament égal : Lab>Do.
4 "fausses" tierces : Mi>Lab, Si>Mib, et surtout
Do#>Fa et Fa#>Sib.
La fausse quinte, ou quinte du loup, est entre Do# et Lab.
Donc, une démarche très proche de celle de Dom
Bedos, à la sauce Schlick.
* "Poïkilorgue" pourrait signifier "orgue
dont l'accord ne varie pas avec la température"
**Michèle CASTELLENGO, chargée de recherche
au CNRS.
Les tempéraments germaniques
Les tempéraments germaniques présentent la particularité d'être des cycles de quintes pures dans lesquels, pour fermer le cercle, on a inclus 3 à 4 quintes totalisant une altération de 1 comma pythagoricien. D'où le qualificatif d'irrégulier donné à ces tempéraments.
Trois périodes se dégagent dans l'histoire des tempéraments germaniques.
La première, celle de Schlick, se caractérise par un compromis
dans le cadre d'un système à la logique régulière.
La seconde, représentée par les systèmes à la Werckmeister, introduit
un retour à la tradition pythagoricienne. La tierce est délaissée au profit
du cycle des quintes, mais la volonté de refermer ce cycle va à l'encontre
de son caractère d'infinité (forme spiralée du cycle Pythagoricien).
La troisième se manifeste par un abâtardissement des systèmes irréguliers
allant dans le sens de l'égalité.
Les systèmes de Kirnberger occupent une place à part, de par la volonté de cet auteur pour la simplicité. C'est l'illustration d'une découverte selon laquelle la soustraction à l'octave de 7 quintes plus une tierce pure laisse un intervalle résiduel égal à la quinte du tempérament égal (quinte pure diminuée du schisma).
En fait, deux logiques s'affrontent : l'une régulière, issue du courant tempéré qui a donné le mésotonique, l'autre Pythagoricienne avec, entre les deux, le système mitigé des vénitiens.
Le tempérament de Schlick - 1511
Arnold Schlick est originaire de la région de Heidelberg.
En 1490 il fuit une épidémie de peste et se retrouve en Hollande. Il est
présent en 1491 à l'inauguration de l'orgue de la cathédrale de Strasbourg.
Il devient, en 1509, organiste du prince électeur du Palatinat à Heidelberg.
Divers auteurs ont fait de Schlick un doux original dans le tempérament duquel on peut voir n'importe quoi (y compris de l'égal ! Ce qui ne peut pas être le cas puisqu'il précise que "ut# est trop bas par rapport à sa quinte ascendante sol#"). En fait, il était opposé à l'usage des feintes brisées (Doppel demitonien) et s'opposa à deux organiers qui espéraient ainsi remédier aux demi tons trop haut ou trop bas, ce qui prouve qu'à son époque on n'utilisait déjà plus le système pythagoricien et qu'on utilisait des tempéraments réguliers mésotoniques.
Le tempérament qu'il décrit s'apparente à celui de Lambert-Chaumont, mais sans tierce majeure pure, les quintes n'étant pas réduites exactement du quart de comma syntonique.
Le principe général de l'accord est de tempérer
les quintes afin que les tierces les plus utilisées qu'elles contiennent
dans leur accord parfait, tant majeur que mineur pour deux d'entre elles,
soient "utilisables". A savoir les tierces : Fa > La (pour
Fa majeur), Ut > Mi (pour Ut majeur), Sol > Si (pour Sol majeur),
Ré > Fa# (pour Ré majeur), La > Ut# (pour La majeur),
Sib > Ré (pour Sib majeur), Ré# > Sol (pour Si majeur),
Fa# > La (pour Fa# mineur), et Ut# > Mi (pour La majeur, déjà
cité). 7 tierces majeures et 2 mineures. Notons qu'il parle de
Ré# qu'il semble privilégier par rapport au Mib pour privilégier
l'accord de si majeur.
Schlick précise que ces tierces seront d'autant meilleures que
celles de Sol# < Mi (en descendant) et Sol# > Si seront mauvaises.
A la fin du cycle de l'accord, il précise aussi que l'Ut# obtenu
est trop bas par rapport à sa quinte ascendante Sol# mais "ça
n'a pas d'importance".
(Donc, une quinte trop forte est sur Ut# > Sol#).
La méthode est loin d'être rigoureuse et repose essentiellement
sur ce qui plait à l'oreille de celui qui pratique l'accord. C'est
un guide pour indiquer ce qui doit plaire en priorité en fonction
des modes musicaux utilisés (tons de l'Eglise).
Les exemples fournis ci-dessous sont des interprétations. (Si vous voulez
consulter l'énoncé du tempérament
de Schlick)
Do
Fa(-1/4)+!(-1/4)+Sol 0- ! (-1/4)+ Sib ! Ré 0- ! (-1/4)+ (Ré#)Mib -------- ! -------- La 0+ ! (-1/4)+ (Sol#)Lab ! Mi 0++ ! (-1/4)+ Do# 0- ! 0- Si Fa# Schlick (d'après D. Devie) Pour ma part, je verrai plutôt, ce qui est encore moins précis: Do
Fa 0-- ! 0--Sol 0- ! 0-- Sib ! Ré 0- ! 0-- Ré#(Mib) -------- ! -------- La 0- ! 0-- Sol#(Lab) ! Mi 0++ ! 0-- Do# 0- ! 0- Si Fa# Schlick (d'après DGW)
Néanmoins ses tierces Fa>La, Do>Mi et Sol>Si sont assez proches de la valeur pure. Lab majeur doit être plus consonant que Mi majeur.
Les tempéraments de Werckmeister
Andréas Werckmeister est né en 1645 et mort à Halberstadt en 1706. Outre
ses activités d'organiste, ce fut un expert en facture d'orgues, un compositeur
et un théoricien prolifique. De nombreux auteurs lui ont réservé une place
importante dans leurs travaux.
Conformément à la tradition inaugurée par Schlick, Werckmeister rejette
vigoureusement l'usage des feintes brisées et le tempérament mésotonique
qui tend à en abuser. Sa démonstration est basée sur le monocorde, ce
qui correspond aujourd'hui à nos modernes accordoirs électroniques de
référence. Le fondement de sa théorie des intervalles est à base 7 et
la hiérarchie va de l'octave à la tierce en passant par la quinte et la
quarte. Sa théorie est assez pythagoricienne et il est clair qu'il s'oppose
aux partisans des tempéraments réguliers qui privilégient la tierce au
détriment de la quinte.
Il a décrit différents systèmes :
- système de gamme naturelle à 20 divisions par octave. Ce système de
gamme naturelle à division multiple est analogue à ceux de Marin
Mersenne et de Zarlino.
- Tempérament mésotonique. Il considère ce système comme vieux et aussi
faux que mauvais.
- Les 3 à 6 sont des tempéraments qu'il juge corrects. Le 3 est le plus
connu, le 4 est considéré comme le mode régulier et le 6 est un tempérament
ésotérique à base 7 .
Le " Werckmeister III "
C'est le plus connu. Les tonalités centrales y sont très bonnes et celles
éloignées sont pythagoriciennes. Ce tempérament centré sur les tonalités
diatoniques a été imité par de nombreux auteurs : Bendeler, Neidhardt,
Sorge et par des modernes tels que Kelletat et Kellner
qui y ont vu le type même du tempérament utilisé par Bach.
On sait que cette formule a été utilisée par le facteur Christoph Kunze
et il n'est pas impossible que celui-ci l'ait montré à Bach après avoir
promis de l'utiliser pour l'orgue de Halle.
Do
Fa 0 ! -1/4 Sol 0 ! -1/4 (La#)Sib ! Ré 0 ! -1/4 (Ré#)Mib -------- ! -------- La 0 ! 0 (Sol#)Lab ! Mi 0 ! 0 (Do#)Réb 0 ! -1/4 Si (Fa#)Solb Werckmeister III
Ici, il ne s'agit pas de répartir le comma syntonique mais le comma
pythagoricien. (Différence entre Si# et Do, Si# étant obtenu par une
succession de quintes pures à partir de Do).
Notons à ce sujet que le schisma est la différence entre le comma
syntonique et le comma pythagoricien. Il est égal à 2/100e de demi-ton
du tempérament égal. (C'est à dire, pas grand chose !).
Un quart de comma pythagoricien est retiré à chacune des trois quintes
de Do à La et le 4e quart entre Si et Solb afin de favoriser les tonalités
en bémol. S'll avait été retiré entre La et Mi, on aurait eu une tierce
Do-Mi presque pure et un tempérament proche de celui que d'Alembert
décrivit 60 ans plus tard. C'est d'ailleurs ce que fera Kirnberger
en 1779.
Exemple musical : Prélude en fa mineur BWV 556, Bach,
Mesure 49 à 54 : L'effet perçu est dû à l'aspect mélodique, Chromatisme
mib-mi-fa de la mesure 50, lab-la-sib de la mesure 52, Broderies autour
du do et du fa des mesures 50 et 52, Accords de fa mineur et de sib mineur
très sombres et opposés à l'effet criard de la tierce pythagoricienne
de la tierce lab-do.
Ecouter
Mesures 63 à 67, Très grande tension provoquée par la dureté de la consonance
du premier accord de chacune des mesures 64 à 66 aboutissant au grand
repos de l'accord de do de la mesure 67.
Ecouter
Le Werckmeister IV
Ce tempérament est donné par l'auteur comme favorable aux tonalités
diatoniques "…si bien que l'on veuille davantage utiliser les modes
réguliers". Il donne aux tonalités diatoniques une agréable ondulation
favorable à la solennité de la musique de Bach.
C'est l'accord qui convient lorsque l'on recherche un certain contraste
entre diatonisme et chromatisme.
Do
Fa 0 ! -1/3 Sol -1/3 ! 0 (La#)Sib ! Ré +1/3 ! -1/3 (Ré#)Mib -------- ! -------- La +1/3 ! 0 (Lab)Sol# ! Mi 0 ! -1/3 (Réb)Do#-1/3! 0 Si (Solb)Fa# Werckmeister IV
Aucune tierce majeure n'est pure.
2 tierces excèdent la valeur pythagoricienne de 1/3 de comma pythagoricien
: Lab>Do, Réb>Fa.
Un très grand ton Lab>Sib.
C'est un tempérament très élaboré dans la mesure où l'auteur ne se contente
plus de "fermer" son cycle de quintes, mais répartit des intervalles de
1/3 de comma pythagoricien (ce qui, déjà, est unique) négatifs dans une
quinte sur deux de Sib à Do# et, comme ça fait -5/3 au total, il en ajoute
deux positifs dans les tonalités élevées pour compenser de -5/3 à -3/3,
soit le comma pythagoricien entier.
Il aurait pu se contenter d'en retirer 3 de do à si. Ce qui serait à rapprocher
des tempéraments italiens à -1/6e de comma sur 6 quintes. Il l'a peut
être fait, mais il n'en parle pas.
Exemple : Fantaisie et fugue en sol mineur BWV 542, Bach,
Mesures 1 à 3, Le passage du lab, du fait de sa proximité avec le sol,
crée un climat douloureux.
Ecouter
Mesures 15 et 16 Broderie expressive autour du si due au petit demi-ton
si>si# et du petit ton si>do#. Le lab du dernier temps de la mesure
15 surprend moins qu'à la mesure 2 de l'exemple précédent, à cause du
contexte harmonique qui lui impose une résolution sur sol.
Ecouter
Mesures 31 à 35 Alternance d'accords consonants avec accords dissonants
du système. Les tierces lab>do, solb>sib et réb>fa sont plus
grandes que les tierces pythagoriciennes qui sont déjà très dures.
Ecouter
Mesures 63 à 67 Dans le contre sujet repris par le ténor, opposition
mélodique des grands demi-tons fa<mi et ré<do# et du petit ton mi<ré
.
Ecouter
Mesures 113 à 115 114 : beaucoup de teinte donnée par les fa# et les
do# très bas. 115 : la hauteur des notes correspond mieux au contexte
harmonique.
Ecouter
Mesures 126 à 129, De par sa nature dans ce tempérament, le lab est
insistant, 128, à la pédale, opposition du très petit ton sib>do et
de l'immense ton lab>sib.
Ecouter
Mesure 135 à 139, on obtient une grande variété de coloris sur les temps
forts et cette instabilité est résolue sur un do mineur confortable.
Ecouter
Le Werckmeister V
Il s'agit d'un tempérament régulier où les principales quintes sont
réduites de 1/4 de comma pythagoricien et avec loup entre Sol# et Mib.
Ce tempérament nerveux manque d'accords paisibles où on aimerait se reposer.
(En fait, il répartit des quarts de comma là où les
autres mettent des quintes pures, afin de favoriser des tonalités peu
usitées. En résultat, plus rien n'est bien consonant - DGW)
Moins1/4 de comma pythagoricien entre Fa>Do, Ré>La, La>Mi, Fa#>Do#
et Do#>Lab.
+1/4 entre Lab et Mib. Les autres quintes sont pures, ce qui fait que
la plupart des tierces usuelles sont pythagoriciennes.
Do
Fa -1/4 ! 0 Sol 0 ! 0 (La#)Sib ! Ré 0 ! -1/4 (Ré#)Mib -------- ! -------- La +1/4 ! -1/4 (Sol#)Lab ! Mi -1/4 ! 0 (Do#)Réb -1/4 ! 0 Si (Fa#)Solb Werckmeister V
Le Werckmeister VI (Septenarius)
C'est un tempérament qui s'inspire de considérations numérologiques sur la magie du nombre 7. C'est une curiosité purement théorique et aucune mention ne fait état d'une quelconque application.
Do
Fa 0 ! -1/7 Sol -1/7 ! -4/7 (La#)Sib ! Ré 0 ! + (Ré#)Mib -------- ! -------- La +1/7 ! 0 (Sol#)Lab ! Mi 0 ! 0 Do#)Réb -2/7 ! -1/7 Si (Fa#)Solb Werckmeister VI
Werckmeister et le tempérament égal.
De 1681 à 1691, Werckmeister ne fait mention que de tempéraments inégaux.
Le tempérament égal n'est décrit qu'à partir de 1697 et, s'il indique
qu'il pourrait être une solution lorsque les incursions dans les tonalités
éloignés se multiplient, la rejette cependant car il note que les musiciens
ne l'acceptent pas. Lui même préfère les tempéraments inégaux qui favorisent
les tonalités diatoniques.
Ce n'est qu'en 1702 qu'il prend parti en faveur du tempérament moderne,
faisant valoir les possibilités de transpositions illimitées et les modulations
enharmoniques qu'il autorise.
Toute la question est de mesurer quelle put être son influence.
A l'époque de Lambert Chaumont, Werckmeister se désolidarise de l'Europe
entière. Il aborde la question d'une manière originale avec l'idée d'un
cycle de quintes fermé sur lui même. Ses prises de position laisse supposer
qu'il ne faisait pas l'unanimité et que des formules régulières (mésotoniques)
étaient encore pratiquées par des praticiens routiniers. Les vues de Werckmeister
suivent une tradition médiévale qui est manifestement la cause de son
pythagorisme relatif.
Gottfried Silbermann (1683 - 1753)
La famille Silbermann fut sans conteste la plus en vue et la plus prolifique
des dynasties de facteurs d'orgues d'Europe.
Gottfried, né en 1683 et mort à Dresde en 1753 a étudié et travaillé avec
son frère Andréas en Alsace. Il s'établit à Dresde en 1711 et eu pour
élève Zacharias Hildebrandt que Bach recommanda à plusieurs reprises.
A dater de 1736, il est connu comme facteur de piano-forte.
Le tempérament qu'il utilisait a fait couler beaucoup d'encre mais sa
manière semble avoir évolué: on lui reprochait un "grand méchant loup".
Le témoignage qui semble le plus fiable au jugement de Dominique Devie
est celui de Sorge. Ce dernier était un partisan du tempérament
égal et fut un témoin direct de la facture de Gottfried.
Silbermann aurait pratiqué un tempérament régulier avec 11 quintes réduites
de 1/6e de comma pythagoricien, la douzième étant affectée d'un loup (Sol#-Mib
trop grand de 5/6e de comma P.).
Sous l'influence de Bach, il aurait évolué vers ce tempérament en partant
du mésotonique au quart de comma qu'il aurait appris en Alsace. (Cette
thèse est contredite mais je ne la trouve pas si mauvaise - DGW).
Il n'y a pas lieu de douter de la description qu'en fait Sorge, seulement
le cheminement pour le réaliser n'est pas évident sans appareillage.
Do
Fa -1/6 ! -1/6 Sol -1/6 ! -1/6 (La#)Sib ! Ré -1/6 ! -1/6 (Ré#)Mib -------- ! -------- La +5/6 ! -1/6 (Lab)Sol# ! Mi -1/6 ! -1/6 (Réb)Do#-1/6! -1/6 Si (Solb)Fa# Gottfried Silbermann
Exemple musical : Prélude et fugue en sol mineur - D. Buxtehude
Les tempéraments de Kirnberger
Né en Thuringe en 1721, Johann Philipp Kirnberger a étudié l'orgue avec JB Kellner. De 1739 à 1741 il a suivi l'enseignement de Bach. Il est mort à Berlin en 1783.
C'est le théoricien allemand de l'harmonie le plus connu. Sa qualité d'élève
de Bach lui a assuré un grand renom. Ses tempéraments inégaux ont fait
le tour du monde dès la fin du 18e siècle. Malheureusement il ne nous
a pas transmis le tempérament de Bach mais des formules conçues en vu
d'une grande simplicité d'exécution.
Kirnberger s'est opposé avec véhémence à certains aspects des théories
harmoniques de Rameau et, entre autre, l'idée que la mélodie est
issue de l'harmonie.
Son opinion sur la valeur artistique du tempérament égal est sans équivoque
: "Le tempérament égal est tout simplement complètement abject".
Les premières mentions de ses tempéraments datent de 1760.
Le tempérament N°2 est daté de 1766 et figure dans un recueil d'exercices
pour clavecin, de même qu'il y aborde le problème des quintes avec le
violon et des intervalles des trompettes.
En 1771, dans "Die Kunst des reine Satzes" l'auteur rappelle sa
découverte que la soustraction à l'octave de 7 quintes pures + une tierce
donne la quinte du tempérament égal (la 8e, qui ferme le cycle, qu'il
place entre Fa# et Réb).
Kirnberger I - 1760
Do
Fa 0 ! 0 Sol 0 ! 0 (La#)Sib ! Ré 0 ! -1 (Ré#)Mib -------- ! -------- La 0 ! 0 (Sol#)Lab ! Mi 0 ! 0 (Do#)Réb 0- ! 0 Si (Solb)Fa# Kirnberger I
Dans ce tempérament Kirnberger retire un comma
syntonique entier entre ré et la, et le schisma
entre fa# et do# (C'est cette quinte qui est identique à une quinte
de tempérament égal, en fait parce que par hasard le schisma est très
proche de 1/12 de comma pythagoricien).
Plus simple à faire, Il n'y a pas ! Do>Sol, Sol>Ré purs, Do>Mi
pur, La>Mi pur puis Mi>Si et Si>Fa# purs.
En descendant, les quintes de Do à Réb toutes pures. La quinte résiduelle
Fa#>Réb doit légèrement onduler à cause
du schisma.
Seulement ce tempérament n'est que l'illustration de sa théorie : 7 quintes + 1 tierce, et ne fut jamais utilisé. En fait, ce n'est pas loin d'un tempérament pythagoricien dont le " loup " serait entre Ré et La. On sait que les tierces qui "contiennent" la quinte tempérée y sont très consonantes. L'abondance de tierces pythagoriciennes (9) contre 3 pures devait le rendre bien dur dans les modulations.
Kirnberger II - 1766
Dans ce tempérament, le plus connu, le comma syntonique est réparti sur deux quintes : Ré>La et La>Mi.
Do
Fa 0 ! 0 Sol 0 ! 0 (La#)Sib ! Ré 0 ! -1/2 (Ré#)Mib -------- ! -------- La 0 ! -1/2 (Sol#)Lab ! Mi 0 ! 0 (Do#)Réb 0- ! 0 Si (Solb)Fa# Kirnberger II
Entre Ré>La et La>Mi, -½ comma syntonique
Entre Fa# et Do# (ou Réb), 0 moins le schisma !
Deux accords majeurs purs : Do>Mi>Sol et Sol>Si>Ré. Les Sib
et Fa 7e ajoutés à ces accords en font des accords de dominante parfaitement
purs, acoustiquement, à cause des tons pythagoriciens Sib>Do et Fa>Sol.
Deux accords mineurs purs : Mi>Sol>Si et Si>Ré>Fa#.
Trois tierces majeures pures : Do>Mi, Sol>Si et Ré>Fa#
Les autres tierces sont soit pythagoriciennes, réduites ou non du schisma,
soit plus grandes que pures du demi comma syntonique.
L'accord est très facile à faire en partant du Do, comme c'était l'usage à l'époque : Do>Sol, Sol>Ré purs, Do>Mi pur, Ré>La et La>Mi égaux en ajustant seulement le La entre les deux ; Mi>Si et Si>Fa# purs, puis, en descendant, des quintes pures de Do à Réb. (On fait des alternances de quartes et quintes, bien sûr, afin de ne se balader que sur une octave : Do>Sol en montant, Sol<Ré en descendant, Ré>La en montant, La<Mi en descendant, etc …sachant que dans une octave, la quarte inférieure doit donner le même nombre de battements que la quinte supérieure)
Le caractère de ce tempérament est dû à un grand contraste entre les accords purs et les accords tempérés.
Exemple musical : Le labyrinthe harmonique BWV591, de
Bach,
Mesures 2 à 6 : Netteté de l'accord de sol et de l'accord de do mesure
3, Même chose mesure 4 avec la septième ajoutée (sib), Ces accords de
do et de sol sont absolument purs, mais cela ne s'est pas fait sans concessions.
La quinte ré>la du premier temps de la mesure 4 fait entendre de forts
battements.
Ecouter
Mesure 15 à 17 : Caractère tumultueux du chromatisme.
Ecouter
Mesures 38 à 42 : Mesure 40, un accord de sol, avec septième majeure,
totalement sans battement, Mesure 41, accord pur de si mineur et, sur
le 3e temps, un si majeur dissonant suivi d'un si mineur pur.
Ecouter
Mesures 49 à 51 :
Ecouter
Kirnberger III - 1779
Ce tempérament résulte de l'adoucissement de la seconde formule, dû
aux remarques de Forkel qui la trouvait trop abrupte.
Il consiste à réduire de ¼ de comma syntonique les 4 quintes de Do à Mi
tout en conservant la quinte schismatique sur Fa#>Do#. Tiens ? on n'est
pas loin de d'Alembert, sauf que les quintes de Mi à Do sont pures, ou
presque pour Fa#>Réb, schisma oblige ! Sauf que ce dernier a délibérément
haussé les quintes montantes pour favoriser Fa#, Do# et Sol#, et, baissé
les quintes descendantes pour favoriser Sib et Mib !
Le Kirnberger III, lui, favorise surtout les bémols.
Ce tempérament est également facile à réaliser : Tierce Do>Mi pure. Répartition de 4 quintes identiques entre Do et Mi en corrigeant par approche le Sol, le Ré et le La. Mi>Si et Si>Fa# pures (Comme pour le mésotonique). En descendant, les quintes Do à Réb pures. A vos claviers ! (Attention : si vous voulez un la à 440, il faut commencer par un Do haussé de 10 cents).
Do
Fa 0 ! -1/4 Sol 0 ! -1/4 (La#)Sib ! Ré 0 ! -1/4 (Ré#)Mib -------- ! -------- La 0 ! -1/4 (Sol#)Lab ! Mi 0 ! 0 (Do#)Réb 0- ! 0 Si (Solb)Fa# Kirnberger III
Exemples musicaux : Choral " Nun Komm… " BWV 599 - Bach
Prélude de la suite anglaise N°3 en sol mineur BWV 808 - Bach
Kirnberger a eu une grande influence en Europe au début du 19e siècle puisqu'on retrouve ses deux premiers tempéraments chez plusieurs auteurs. Certains se réclament ouvertement de lui. D'autres se sont inspirés de sa seconde formule comme ce fut probablement le cas de Bruder en 1829
Exemple : Choral " Nun Komm… " BWV 599 - Bach
Mesures 4 à 7 : Mesure 5, parfaite consonance de l'accord de fa majeur
(à cet endroit le texte parle de Jésus, enfant reconnu de la vierge).
Ecouter
Spéculations sur le tempérament de Bach
Voir aussi "Les
orgues du temps de Bach",
un texte de Marc Garnier in "Les facteurs d'orgues Français"
N°10.
De nombreux auteurs ont tenté de reconstituer le tempérament inégal de Bach.
H Kelletat
Kelletat en a donné un à plusieurs reprises entre 1960 et 1977. Il ne
justifie pas sa proposition mais établit une relation entre Bach et Kirnberger.
Ce dernier avait affirmé qu'il avait bien transmis l'enseignement de son
maître. Kelletat en a fait dériver sa propre proposition du 3e tempérament
de Kirnberger décrit dans une lettre à Forkel en 1779. C'est oublier que
Kirnberger avait décrit en 1760 un système graphique de tempérament égal
et composé un "Musicalischer circul" passant par toutes les tonalités.
Sa proposition ressemble un peu à la proposition N°3 de Neidhardt, ce
qui la rend plausible, sans plus.
La description de l'égal par Kirnberger ne reflète pas forcément une adhésion
à ce système. Loin de là ! La transmission de l'enseignement de son maître
concerne de toute évidence son système harmonique et non ses tempéraments.
Barbour
En 1951, Barbour a indiqué la possibilité d'utiliser l'inégal, sans proposer de solution particulière. Cette position a également été adoptée par Jorgensen en 1977.
Barnes
En 1979, Barnes s'est basé sur une étude statistique du contenu harmonique de oeuvre pour clavier de Bach en classant les tierces des 24 préludes du "CBT" par ordre de prééminence. Il a réalisé un tempérament où ces tierces sont favorisées d'après une procédure mathématique de Hall (1973-74). Que penser des méthodes statistiques dans ce domaine ?
Di Veroli
Dans une réponse à Barnes (1981), di Veroli propose le tempérament de Vallotti-Barca ou de Young sans se souvenir qu'une formule de ce genre avait été construite par Werckmeister (6 quintes de fa à si réduites de 1/6 de comma pythagoricien, les 6 autres quintes sont pures). Il existe suffisamment de tempéraments historiques sans avoir besoin d'en inventer de nouveaux.
Kellner
Kellner est un ésotérique qui a fait appel à la mystique des nombres.
Il a le mérite de faire appel à des considérations théologiques qui ne
sont pas dénuées d'intérêt.
Les tensions polyphoniques dans oeuvre de Bach sont à mettre en rapport
avec le caractère tourmenté de la mystique de Luther. Sa musique traduit
un caractère exubérant d'inspiration végétale comme le style gothique
et une tension permanente sur fond de réalisme (simplicité évangélique).
Ce climat exige un tempérament inégal afin de favoriser les périodes de
repos.
Si la graphie gothique a subsisté en Allemagne jusqu'à la dernière guerre
et si le monde germanique a préféré des tempéraments largement pythagoriciens,
c'est dû à cette sensibilité médiévale, perceptible dans l'art luthérien
typique de l'Allemagne du nord.
Le tempérament utilisé par Bach devrait donc avoir deux caractéristiques
: être assez chaleureux tout en favorisant les tensions. Deux des tempéraments
de Werckmeister présentent ces particularités.
Kellner voulait que l'Ut majeur prenne sur lui la plus grande et unique
perfection, qu'il met en rapport avec la trinité. La mise en relation
de l'accord parfait majeur avec le dogme chrétien, comme symbolisant "
l'unitas " par rapport à la triade mineure imparfaite est une vieille
rengaine. Elle vient de Lippius (17e siècle) et en France on trouve une
allusion à ce prétendu symbolisme chez Moucherel qui écrivait en 1734
"Je regarde l'Ut comme le père, le Mi comme le fils parce qu'il est
le plus près de l'Ut et le Sol pour le saint esprit…ces trois sons sont
bien unis ensemble…".
Les justifications de Kellner reposent sur le "traité de la basse chiffrée"
rédigé par Bach en 1738. La triade tempérée majeure ne peut apparaître
qu'une seule fois dans son état de plénitude maximum de sorte que l'on
a conclu que le meilleur accord devait être celui d'Ut majeur. Les autres
devant s'écarter peu à peu du prototype, Kellner reproche à Kirnberger
d'avoir mis une tierce pure sur Ut, ce qui exclut toute possibilité d'étagement
progressif. Werckmeister serait coupable, lui, de n'avoir pas suivi la
logique du système jusqu'au bout.
Le tempérament de Kellner est très intéressant musicalement et comprend 7 quintes pures, 5 quintes tempérées de 1/5 de comma pythagoricien, pas de tierce pure mais Ut majeur privilégié, 7 tonalités pythagoriciennes : Fa#, Ut# et Sol# majeur, Mib, Sib, Fa et Do mineur. C'est un hybride du Werckmeister III et du Kirnberger III.
Do
Fa 0 ! -1/5 Sol 0 ! -1/5 (La#)Sib ! Ré 0 ! -1/5 (Ré#)Mib -------- ! -------- La 0 ! -1/5 (Sol#)Lab ! Mi 0 ! 0 (Do#)Réb 0 ! -1/5 Si (Fa#)Solb Kellner (1982)
Exemple musical : Prélude et fugue en ut majeur BWV 846 (CBT)
on a un bon exemple de l'incidence que peuvent avoir les différentes consonances
d'intervalles sur le rythme. Mesure 14 la sixte la-fa du 3e temps fait
entendre rapidement assez de battements en comparaison avec la tierce
do-mi du 4e temps suivant. Ce type d'alternance oblige inconsciemment
notre oreille à percevoir une pause plus importante sur certains accords.
Bradley Lehman
Bradley Lehman se base sur le dessin du frontispice du manuscrit du "clavier bien tempéré" qu'il lit comme le canevas d'un tempérament pensé pour ces 24 préludes et fugues.
En retournant le dessin, Lehman y voit la succession de la valeur des quintes en fonction de la taille des boucles :
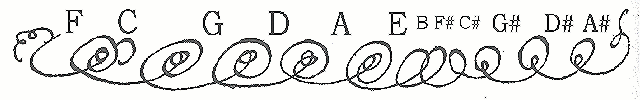
- 5 quintes diminuées d’un sixième de comma (pythagoricien)
entre Fa et Mi.
- 3 quintes pures entre Mi et Do#.
- 3 quintes plus petites d’un douzième de comma entre Do#
et Ré#.
- 1 quinte légèrement augmentée d’un douzième
de comma entre Si bémol et Fa.
Emile Jobin, éminent Facteur de Clavecins, donne une autre
interprétation qui est à son tour discutée par Philippe
Allain-Dupré, éminent flûtiste, lui. Emile
Jobin y voit des tierces pures, ce que réfute Allain-Dupré.
La démarche est intéressante mais, faute de consensus, il
y aura lieu de se référer directement aux sites de chacun
d'eux pour se forger une opinion :
Pour Bradley Lehman ,
pour Emile Jobin ,
pour Allain-Dupré .
Les tempéraments italiens
Souvenons nous tout d'abord que ce qu'on appelle l'Italie maintenant était à l'époque une mosaïque de petits états aux particularismes prononcés. Au 18e siècle, les centres les plus brillants de la vie musicale furent Venise et Naples. De nombreux témoignages indiquent que le tempérament en usage jusqu'au milieu du 18e siècle était le tempérament régulier mésotonique au quart de comma syntonique.
Antegnati
Antegnati décrit en 1608, sans erreur possible, un tempérament régulier de ¼ de comma.
Cavalliere, en 1634, confirmait que les tierces doivent être " aussi parfaites que possible ". Suivent des références d'auteurs du même avis tels que Aaron, Foliano, Zarlino, etc.
Becatelli
En 1726, dans une lettre, Becattelli fait allusion à un tempérament régulier à 1/5e de comma. Avec divers autres témoignages, on pourrait en déduire que Bartolomeo Cristofori, l'inventeur du pianoforte, utilisait ce tempérament. Il est fort possible qu'il fut même l'accord ordinaire de la région vénitienne, si on en croit Riccati. Mais Barca a été très critique à son sujet. Les systèmes réguliers de 1/4 à 1/6e de comma semblent s'établir solidement en Italie jusqu'au milieu du 18e.
Venise, au 18 et au 19e siècle.
Le tempérament régulier en usage dans la région devait être plus proche
de ceux à 1/5e ou à 1/6e de comma. Les variations semblaient varier selon
l'humeur de l'accordeur et selon l'idée qu'il se faisait d'un " tono
medio " qui était alors la norme.
Le système tempéré égal ne s'est pas imposé partout avant 1885 en Lombardie
- Vénétie. Après 1802, il est très probable que les écarts entre les systèmes
se soient rétrécis. En 1870, le facteur d'orgues De Lorenzi propose encore
un tempérament " modéré " au 1/8e de comma. 40 ans plus tôt, cette dérive
s'était produite pour le pianoforte, tel qu'en atteste " la gazette
de Venise " d'alors.
Naples
Dans la région napolitaine, la pratique d'un tempérament régulier au
quart de comma est attesté en 1634.
Naples est resté un bastion de l'inégalité, le pianoforte n'a pas eu pour
conséquence la généralisation du tempérament égal, bien au contraire.
En 1835, Sievers, facteur de pianoforte, applique une formule au 1/5 de comma sur les 5 quintes de Do à Mi. Les autres sont pures. Ce tempérament est proche de celui de Barca et peut être défini comme un intermédiaire entre le Kirnberger III et celui au 1/6e de comma à l'italienne. En 1868, le tempérament de Sievers est toujours utilisé dans l'atelier de Luigi Mascitelli. Ce dernier précise que ce système est utilisé couramment à Naples depuis 30 ans.
Dans tous les autres royaumes d'Italie, on assiste à des démarches plus ou moins similaires.
Tartini - Vallotti - Barca
En 1735, le père Vallotti estimait que l'accord du clavecin était imparfait.
Il demanda (indirectement) à Riccati qui était un grand acousticien,
de lui déterminer un tempérament moins imparfait que celui en usage. La
formule qui en résultera, étant un ouvrage collectif, en fait le tempérament
"Tartini, Vallotti, Barca" du nom de ses principaux promoteurs.
Il restera à la base du tempérament vénitien.
Il s'agit de répartir le comma syntonique (81/80) entre les 6 quintes
"des touches longues" et le schisma entre les six quintes des "touches
courtes". Cette pratique est justifiée par le fait que "les touches
longues sont en usage continuel dans la musique".
(Tout le monde aura compris que les touches longues
sont les notes diatoniques et les touches courtes, les feintes).
Après s'être opposé explicitement au tempérament égal, Vallotti retient
la solution qui consiste à accorder "chacune des quintes des touches
courtes … dans son juste intervalle de 2/3".
La première mention du tempérament de Vallotti figure dans le "Trattato
de musica" de Tartini, en 1754. Le Traité de Vallotti lui même
n'a pas été publié de son vivant.
La formule de base de ce tempérament consiste à retirer 1/6 de comma syntonique
à toutes les quintes entre Fa et Si et d'accorder les 6 autres pures.
Mais, comme il utilisait le comma syntonique, il a tout bonnement négligé
le schisma dans ses calculs, lequel affecterait la quinte Sib>Fa compte
tenu de l'ordre dans lequel il pratique l'accord.
Barca, en 1802, précise ce tempérament en tenant compte d'un schisma partagé. C'est pour cette raison qu'on a cru longtemps que Vallotti partageait le comma pythagoricien. En fait, c'est bien le comma syntonique qui est le point de départ chez tous les auteurs italiens. Il n'y a aucun doute et Vallotti a pris le parti délibéré de négliger cette différence pour simplifier son exposé.
Do
Fa -1/6 ! -1/6 Sol 0 ! -1/6 (La#)Sib ! Ré 0 ! -1/6 (Ré#)Mib -------- ! -------- La 0 ! -1/6 (Sol#)Lab ! Mi 0 ! -1/6 (Do#)Réb 0 ! 0 Si (Fa#)Solb Tartini - Vallotti - Barca
Notons que Pierre Yves Asselin fait commencer la série
des quintes tempérées sur Do. En fait, c'est du Fa qu'il s'agit, nous
précise Dominique Devie.
Le schisma partagé consisterait à retirer 0,01 comma aux quintes "pures".
En réalité, on fait un peu comme on le sent. En effet, dans son troisième
mémoire, Barca précise que la façon de procéder des accordeurs italiens
est loin d'être rigoureuse, lesquels "… ont appris le métier sans le
connaître …".
Le mésotonique au quart de comma et ce système sont les pôles entre lesquels tous les accords vénitiens devaient se situer, avec probablement toutes les nuances intermédiaires.
Exemple musical : Sonate K 115 - Domenico Scarlatti
En Espagne,
Peu de sources, surtout des relevés sur des orgues anciennes (plus de
100 ans après leur construction, par Chéron).
Les formules que propose Dominique Devie d'après ces relevés
sont assez folklo !
Il est fort probable que les rapports que l'Espagne entretenait avec l'Italie
ont fait que des tempéraments semblables y ont été pratiqués.
En Angleterre,
Difficile de savoir si, à l'époque médiévale, on utilisait les rapports
purs ou un pythagoricien. Les tierces pures y ont été adoptées entre 1413
et 1480.
Culturellement très proche de la France, cela laisse supposer qu'en France
aussi, les tierces pures auraient été adoptées dans cette période, et
par là même, dans tout l'Europe. Même si l'Angleterre se prétend première
en ce domaine.
En 1694, Holder décrit un tempérament au quart de comma syntonique très
semblable à celui de Lambert-Chaumont.
Difficile de jouer 6 des 8 suites de Haendel avec un tempérament mésotonique, surtout quand on y voit apparaître des Mi# et des Si#. La solution se trouve dans "Le petit Larousse illustré" qui nous rappelle que Haendel est un compositeur allemand qui passa la majeure partie de sa vie à Londres. Les suites ont été publiées à la même époque que le "Clavier bien tempéré". Il devait avoir un "Werckmeister" dans sa valise.
Les sources que passe ensuite en revue Dominique Devie démontrent que
l'Angleterre a été le siège d'un nombre incroyable de tempéraments issus
de toutes origines, tout musicien d'origine étrangère venant suppléer
à l'indigence de la production locale (ça, c'est moi qui le dis !).
Rien de bien sérieux ni de bien original : on navigue entre des tempéraments
à la d'Alembert, à la Tartini, à la Werckmeister …
Il faut attendre 1875 pour que l'égal soit adopté pour les orgues.
Aux Etats-Unis,
Deux écoles : celle de Pennsylvanie, qui a pour origine des facteurs d'origine allemande et qui a adopté très tôt le système égal, dès 1764, sous l'influence de Sorge. Avant, on y rencontrait surtout des accords à la Silbermann.
L'école de Boston, qui tient ses origines de l'Angleterre, appliquait des systèmes au quart et au 1/5e de comma assez composites. Ce n'est qu'en 1866 que l'égal est définitivement adopté.
Le tempérament égal
Les dates de l'histoire du tempérament égal:
1595: le chinois Chou Tsai Yu aurait calculé les intervalles
tempérés avec une bonne proportion.
1600: Simon Stevin, un flamand, aurait accordé un monocorde avec une bonne
approximation.
1626: Le sieur Gallé tente de convertir le facteur d'orgue belge
Séverin au tempérament égal.
Jacques Boesman a bénéficié d'un système à division multiple déjà décrit
par Costeley en 1570 et dont Gallé se prétendait inventeur.
1636: Mersenne a rempli une bonne partie de "l'harmonie universelle"
de calculs relatifs au tempérament égal en précisant que les praticiens
de son temps ne sont pas d'avis de changer l'accord de l'épinette pour
la contraindre à celui du luth (égal) "de peur de quitter la perfection
de leurs tierces". Quant aux calculs de Mersenne, il faut encore les
piger !
1640: Doni, faisant allusion à l'ignorance de Frescobaldi, s'oppose
à la tentative d'un vieillard calabrais d'acclimater le tempérament égal
à Rome.
1642-45: Pier Francesco Valentini propose dans plusieurs manuscrit
le tempérament égal qu'il prétend être le seul à le réaliser exactement.
Juraj Krizanic, de passage à Rome, propose un dispositif de transposition
en relation avec le tempérament égal.
1650: Jean Denis nous confirme l'échec (à Paris, cette fois) du
sieur Gallé en dénonçant l'imposture d'une prétendue invention du tempérament
égal par ce dernier.
1668-82: Juan Caramuel Lobkowitz milite en faveur du tempérament
égal. Il serait le premier à l'avoir calculé avec une méthode logarithmique.
On trouve un écho de cette agitation purement théorique chez G Sabbatini.
1674: Le père jésuite Zaragova témoignerait d'une expérimentation
du tempérament égal sur des orgues de Valence et de Madrid.
1692: Le Japonais Nakane aurait trouvé la valeur de 0,94 qui est
une bonne approximation du rapport inverse.
1702: Werckmeister aurait été partisan du tempérament égal. C'est
vrai, mais uniquement dans ses derniers écrits, et sans influence sur
ses contemporains.
1722: Bach compose son CBT dont on a voulu faire un manifeste du
tempérament égal. Qu'en est-il exactement? "Bien tempéré"
ne signifie pas obligatoirement "égal".
La même année, à Dresde, Suppig compose un "labyrinthus musicus" conçu
pour un clavier mésotonique étendu.
1737: Rameau s'enflamme pour le tempérament égal. Il propose la
mithridatisation par accoutumance comme remède à l'agressivité des tierces
de ce tempérament. Agité par un sursaut d'honnêteté, il reconnaît la monotonie
que le tempérament égal possède "au suprême degré" (sic).
1754: D'Alembert souligne la versatilité de Rameau et estime qu'il
appartient à chacun d'opter selon son goût.
Gallimard entend toujours par "quinte tempérée" une quinte réduite de
1/4 de comma.
1756: Marpurg, spécialiste du persiflage, déclare qu'il lui semble
que "c'est une musique très mince que celle qui ne doit son mérite qu'au
petit marteau de l'accordeur".
1760: Kirnberger (élève de Bach) commence par décrire une méthode
graphique conduisant au tempérament égal, qu'il juge somme toute "tout
simplement complètement abject".
1767 Rousseau raille "l'air scientifique" de la formule de Rameau,
tout en se faisant le promoteur des utopies égalitaires.
1776: Dom Bedos manifeste sa résistance au tempérament égal. Il
se plante, d'ailleurs, dans les calculs qu'il a fait pour ne pas paraître
idiot devant la caste naissante des "mandarins de la science".
1779: Kirnberger fait répondre à Marpurg que ses traits d'esprit
sont pitoyables "pour faire entrer Bach et Telemann dans son jeu" en faveur
du tempérament égal.
1780: De Cryseul prend parti en faveur du tempérament égal de Rameau
et propose son monocorde.
1782: L'italien Pizzati propose encore un tempérament à la d'Alembert
qui sera repris par d'autre écrivains.
1801: Blanchet est censé donner une partition égale mais elle est
encore subtilement inégale.
De même pour Godin qui dit que la tierce si-ré# doit être plus
forte que les autres.
1802: L'italien Dall'Ollio condamne les tempéraments "capricioso"
et, après avoir fait profession de foi en faveur du tempérament égal,
se plante lamentablement dans ses calculs.
1816: L'italien Asioli prend à parti les facteurs d'orgue coupable
de résister au tempérament égal.
1829: Bruder rapporte les propos du Père Jacob de Saint Margen
à propos du tempérament égal: "Maintenant que le loup est dans tous
les tons, l'ange ne peut plus descendre". Il est encore dit qu'utiliser
le tempérament égal revient "à manger tous les jours la même chose".
1833-36: Cavaillé-Coll répand le système égalitaire et encore,
en 1841, pratique-t-il un tempérament subtilement inégal
à l'orgue de Saint-Denis .
Montal publie deux opuscules à la gloire du tempérament égal.
1844: L'éditeur italien Ricordi propose un instrument pour accorder
les piano-forte au tempérament égal.
1845: L'italien Barbi, de l'école de Padoue, déclare nuisible le
tempérament égal.
1849: Hamel, dans son encyclopédie, écrit "On a généralement
adopté ... pour partition, celle par tempérament égal. Ce mode de tempérament,
qui parait le plus rationnel, a cependant l'inconvénient de n'admettre
aucun intervalle juste ... où l'oreille péniblement affectée par la dureté
des tierces puisse se reposer".
1851: A Londres, tous les orgues, y compris ceux de l'exposition universelle,
sont toujours à l'ancien tempérament inégal.
1853: La firme Gray et Davison accorde pour la première fois un orgue
au tempérament égal.
1860: Filippi, critique chez Ricordi, fait part de son désenchantement
face au tempérament égal pour le piano-forte.
1868: Les napolitains restent fidèles à un tempérament à 1/5 de comma
pour le piano-forte.
1869: Americo Barberi prêche un nouvel ordre moral et dénonce comme
ayant de mauvaises moeurs les facteurs d'orgues qui préfèrent le tempérament
inégal .
1870: Le facteur d'orgue De Lorenzi publie une formule d'un tempérament
modéré destiné à écarter le recours au tempérament égal.
1880: Le Chevalier Pacifico Inzoli de Crema s'emploie à populariser
le tempérament égal, non sans passer pour un bouffon.
1894: Avoni recense les méthodes de réalisation du tempérament
égal les plus exotiques.
1895: Lavignac mentionne que, transposée en ut, la berceuse de
Chopin conçue en ré bémol devient crue et plate.
1906: Busoni voit dans le tempérament égal un "expédient de
force majeure" et estime qu'il s'agit d'un des maux de la civilisation.
1907: Un accordeur américain reconnaît que le tempérament égal est encore
un mythe.
Saint-Saens considère que le tempérament égal est "un tyran
dévastateur et une hérésie ...". Il reconnaissait toutefois que cette
hérésie "a été trop féconde pour qu'il soit permis de le déplorer".
1942: Ricordi ressort de ses cartons de 1832 une méthode d'accordage inégal
où FA et Mib sont de meilleure tonalité qu'UT.
Le tempérament égal:
Comme l'indique son nom, dans le tempérament égal tous les intervalles sont égaux. Les tierces majeures sonnent toutes "nerveuses" du fait de la réduction de 1/12e de comma pythagoricien de toutes les quintes.
Do
Fa -1/12!-1/12 Sol -1/12 ! -1/12 La# Sib ! Ré -1/12 ! -1/12 Ré# Mib -------- ! -------- La -1/12 ! -1/12 Sol# Lab ! Mi -1/12 ! -1/12 Do# Réb-1/12!-1/12 Si Fa# Solb Egal
L'égal est le système d'accord le plus difficile à réaliser.
La partition commence par le la de référence et se réalise entre
les notes fa2 et si3.
Il consiste à réduire les quintes de 1/12e de comma pythagoricien. Les
vérifications se font par observation de la régularité de tierces successives
(fa-la, fa#-la#, sol-si, etc.), des accords formés d'une tierce mineure
surmontée d'une quarte et des accords formés d'une quarte surmontée d'une
tierce majeure.
Si l'on arrive pas à refermer convenablement le cycle de quintes tempérées
(sur ré-la), il vaut mieux tout recommencer.
Asselin estime que : "On a tout intérêt à " resserrer " légèrement les octaves en profitant du phénomène qui consiste à les entendre toujours pures alors qu'elles sont un peu petites (tolérance de justesse)".
Au 18 et au 19e siècle, des méthodes empiriques consistaient à utiliser
le cycle de 3 tierces qui devaient être identiques, et, à partir de ces
3 tierces, de répartir les 4 quintes complémentaires qui composent ces
tierces.
Par exemple : la - do# - fa - la
Mercadier donna une méthode consistant à faire 11 quintes altérées
de suite, la 12e servant de preuve (comme Asselin ci-dessus) mais il rejette
cette méthode comme longue et incertaine. Il préconise plutôt deux demi
suites tel que : ut à ut# en montant et ut à lab (sol#) en descendant
et précise que l'ut# doit être en accord avec le sol# et que, s'il s'en
fallait un peu, l'inconvénient ne serait pas grand attendu que cette quinte
ne se joue pas souvent.
On tolérait donc des erreurs qui se produisaient sur l'ancienne zone de
la quinte du loup.
Le procédé de la division par tierces a été préconisée par Neidhart
en 1706 et repris par Sorge et Marpurg.
Pour que les tierces obtenues soient bien égales entre elles, il est nécessaire
que la progression de vitesse de leurs battements soit de 25% par degré.
Hamel, dans son encyclopédie (Roret 1849), reproduit intégralement
le texte de "l'art du facteur d'orgues" de Dom Bedos, y compris
le tempérament mésotonique.
Dans le complément écrit de sa main, il précise :
"On a généralement adopté ... pour partition,
celle par tempérament égal. Ce mode de tempérament,
qui parait le plus rationnel, a cependant l'inconvénient de n'admettre
aucun intervalle juste ... où l'oreille péniblement affectée
par la dureté des tierces puisse se reposer". Il en explique
la raison : "... les intervalles de tierce et de quinte, lorsqu'ils
sont justes, produisent un son
résultant
qui est à l'octave ou à la double octave en dessous de la
note la plus grave de l'accord d'où il provient. Autant cette consonance
est agréable, autant est pénible la sensation causée
par des accords dont les intervalles sont altérés ... Dans
ce cas les coïncidences des vibrations ne donnent plus la tonique
de l'accord générateur mais un son qui s'en éloigne
plus ou moins".
Dans le procédé de division de l'octave en trois tierces
qu'il nous propose, il fait l'erreur de vouloir que les trois tierces
soient toutes de même qualité : ".. elles fassent autant de battements
l'une que l'autre et que la dernière ne soit pas plus dure que la première…".
Dans ce cas, seule la tierce centrale aurait la valeur voulue. Le tempérament
n'est pas totalement symétrique et par là même quelque peu inégal, en
favorisant les bémols.
Cette inégalité a été attestée par deux témoignages concordants, l'un
venant d'Italie (Naples 1882), l'autre d'Amérique (Philadelphie 1907).
Hamel le constate d'ailleurs lui même, dans la préface de
son encyclopédie : "... nous avons toujours trouvé
quelques tons plus favorisés que d'autres".
Au début du XXe siècle, la pratique de l'égalité n'était qu'un simple voeu. Des réflexions d'accordeurs jusqu'à l'avènement des accordoirs électroniques étaient analogues (vers 1960).
Accordoir électronique
L'utilisation d'accordoirs électroniques donne des accords assez "plats" dans l'ensemble, annulant définitivement tout caractère tonal. Les accords "à l'oreille" font la part d'une inégalité plus ou moins accidentelle qui n'enlève rien à la musique, bien au contraire et n'interdit pas, sur cette base, d'élargir les octaves empiriquement (alors que Asselin les préconise resserrées).
Toutes les observations à ce sujet montre que l'égalité est restée fort longtemps pure fiction.
Le "tempérament égal à quintes justes" de Serge Cordier
Les accordeurs de la maison Pleyel faisaient la partition dans l'octave
de fa en s'efforçant de contrôler l'égalité des demi-tons par les tierces
et les sixtes. "Mais c'est, nous dit Cordier, ce qui m'a mis
sur la voie d'un nouveau tempérament : Si on fait l'octave parfaitement
pure, la sixte lab-fa battrait nettement moins rapidement que la tierce
réb-fa. Or si on parvient à égaliser la rapidité de battement de ces deux
rapports, on obtient un bien meilleur accord. Les quintes sont plus magnifiques,
les 10e et les 17e également, tout devenait beaucoup plus joli".
La partition de Cordier consiste, à l'intérieur d'une quinte pure fa>do,
à égaliser tous les demi-tons qui s'y trouvent par le biais d'un contrôle
sur les 4 tierces majeures et les 5 tierces mineures de cette quinte.
Ensuite, l'auteur extrapole à partir de chaque note de cette quinte, par
quintes pures ascendantes et descendantes, sur toute l'étendue du clavier.
Ceci donne automatiquement un élargissement des octaves de 1/7e de comma
pythagoricien, élargissement qui rattrape le décalage nécessaire avec
la justesse physique pour satisfaire l'oreille dans les intervalles extrêmes.
En outre, elle compense le phénomène d'inharmonicité des cordes graves
du piano.
Dominique Devie précise que les facteurs d'orgues sont réticents à cette partition mais il estime qu'on pourrait être fort agréablement surpris du résultat. Peut-être évitera-t-on, dit-il, par ce moyen que les mixtures ne deviennent criardes dans l'aigu lorsque les orgues sont strictement accordés au tempérament égal. Celles-ci, ajoute-t-il, provoquent rapidement la satiété des organistes qui n'ont pas les oreilles complètement bouchées.
FIN